【偏差値65以上を目指す中学生へ】
入試過去問を、単元別でかつ正答率の低い問題だけを厳選。
時間のない受験生にとって、自分の苦手単元をピックアップでき、自分の偏差値に合わせた差がつく問題のみを解くことができるようにした。是非チャレンジしてみてね。
千葉県の公立高校入試の前期・後期の仕組み
・後期入試の方が簡単。基本問題への配点も高い。(前期の平均点+20≒後期の平均点)
前期
50分×5教科
各教科100点満点、合計500点満点
後期
40分×5教科
各教科100点満点、合計500点満点
中1
比例と反比例
正答率44.6%
関数 $ y=\frac{12}{x} $ について,xの値が1から4まで増加するときの変化の割合を求めなさい。
xの増加量は、3
x=1のときy=12,x=4のときy=3だから,yの増加量は-9
よって、-3
数の規則性
正答率30.4%
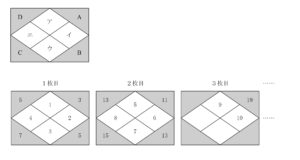
図のように,ア,イ,ウ,エと,A,B,C,Dの8つの部分に分けたカードがたくさんある。
1枚目のカードには,ア,イ,ウ,エに,1から順に連続する4つの自然数1,2,3,4をそれぞれ書く。また,アとイに書いた自然数の和である3をAに,イとウに書いた自然数の和である5をBに,ウとエに書いた自然数の和である7をCに,エとアに書いた自然数の和である5をDに,それぞれ書く。
2枚目のカード以降も,この規則にしたがって自然数を書いていく。
(n+1)枚目のイの部分に書かれる自然数を,nを用いた式で表しなさい。
1枚目のカードには,ア,イ,ウ,エに,1から順に連続する4つの自然数1,2,3,4をそれぞれ書く。また,アとイに書いた自然数の和である3をAに,イとウに書いた自然数の和である5をBに,ウとエに書いた自然数の和である7をCに,エとアに書いた自然数の和である5をDに,それぞれ書く。
2枚目のカード以降も,この規則にしたがって自然数を書いていく。
(n+1)枚目のイの部分に書かれる自然数を,nを用いた式で表しなさい。
よって,4n+2
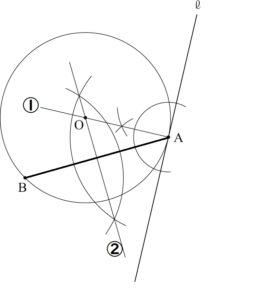
平面図形(作図)
正答率28.9%
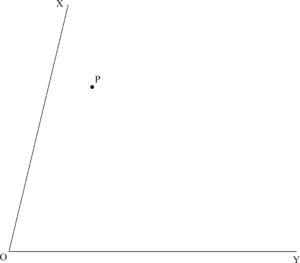
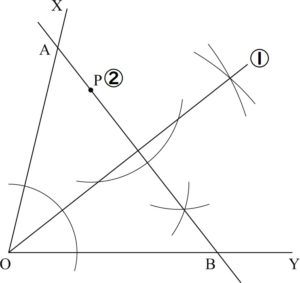
図のように,半直線OX,OYと点Pがある。点Pを通る直線をひき,半直線OX,OYとの交点をそれぞれA,Bとする。このとき,OA=OBとなるように直線ABを作図しなさい。また,2点の位置を示す文字A,Bも書きなさい。
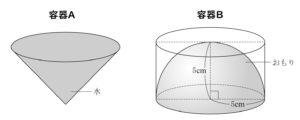
空間図形
正答率18.7%
底面の半径と高さがともに5 cmの円錐の形をした容器Aがある。
また,底面の半径と高さがともに5 cmの円柱の形をした容器に,半径5 cmの半球の形をしたおもりを入れたものであり,これを容器Bとよぶことにする。
容器Aに入っているすべての水を,容器Bに静かに移していく。
このとき,容器Bから水はあふれるか,あふれないかを答えなさい。ただし,その理由を式とことばで書き,答えること。
また,底面の半径と高さがともに5 cmの円柱の形をした容器に,半径5 cmの半球の形をしたおもりを入れたものであり,これを容器Bとよぶことにする。
容器Aに入っているすべての水を,容器Bに静かに移していく。
このとき,容器Bから水はあふれるか,あふれないかを答えなさい。ただし,その理由を式とことばで書き,答えること。
$ 5^2×π×5×\frac{1}{3}=\frac{125}{3}π $
容器Bに入る水の体積は,円柱の容器の容積から半球のおもりの体積をひいた差だから
$ 5^2×π×5-\frac{4}{3}π×5^3×\frac{1}{2}=\frac{125}{3}π $
①と②は等しいので,容器Bから水はあふれない。
正答率6.9%
底面の半径と高さがともに10 cmの円錐の形をした容器Aがあり、図は、水面の高さが9 cmになるまで水を入れたものである。
その中に底面の半径が4 cmの円柱の形をしたおもりを,底面を水平にして静かに沈めると,容器Aから水があふれ出たあと,円柱の形をしたおもりの底面と水面の高さが等しくなった。
このとき,容器Aからあふれ出た水の体積を求めなさい。
その中に底面の半径が4 cmの円柱の形をしたおもりを,底面を水平にして静かに沈めると,容器Aから水があふれ出たあと,円柱の形をしたおもりの底面と水面の高さが等しくなった。
このとき,容器Aからあふれ出た水の体積を求めなさい。
=(高さが9 cmの円錐の体積)+(半径が4 cmの円柱の体積)-(10 cmの円錐の体積)
$ 243π+96π-\frac{1000}{3}π=\frac{17}{3}π $
中2
確率
正答率41.6%
数直線上の2の位置に点Pがある。大小2つのさいころを同時に1回投げ,大きいさいころの出た目をa,小さいさいころの出た目をbとする。点Pは数直線上を右方向にaだけ移動したあと,左方向にbだけ移動する。
このとき,絶対値が2以下の範囲に,点Pが止まる確率を求めなさい。
このとき,絶対値が2以下の範囲に,点Pが止まる確率を求めなさい。
よって、 $ \frac{5}{9} $
-120x120.jpg)
.jpg)