次の単元へ
物理基礎②《力の種類と運動の法則》
【高校物理・物理基礎】~目次~
力学Ⅰ
物体の運動(物理基礎)⇒現在はここのページ
落下運動
力のつり合い(物理基礎)
運動の法則(物理基礎)
剛体にはたらく力
力学的エネルギー(物理基礎)
力学Ⅱ
運動量の保存
円運動
単振運動
万有引力
熱力学
熱とエネルギー(物理基礎)
気体の法則と分子運動
気体の内部エネルギーと状態変化
波動
波の性質(物理基礎)
音波(物理基礎)
光波
電気
電場と電位
コンデンサー
電流(物理基礎)
磁気
電流と磁場
電磁誘導
交流と電磁波
原子
電子と光
原子の構造
原子核と素粒子
教科書レベル重要問題《運動の表し方》
速さと速度の違い
例題
右向きを正方向として,
左向きに速さ 20m/s で走る物体の 速度はいくらか。
解答表示
変位と道のりの違い
*数学のベクトル(向きと大きさを持った矢印)をイメージ。
例題
右向きを正方向として,
小球が点 O を出発して,右へ 50m 進んだ後,左へ 20m だけ移動した。
このとき,小球の点 O からの変位と道のりを求 めよ。
解答表示
道のり:70m
物理で出てくるグラフ(x-tグラフ、v-tグラフ)
★x-tグラフとは
変位xをy軸、時間tをx軸にとったグラフのこと。
⇒傾きが速さを表していることを暗記しよう!
変位x ÷ 時間t =速度 より、
傾き(yの増加量÷xの増加量)が、ちょうど速度を表現しているグラフとなっている。
★v-tグラフとは
速度vをy軸、時間tをx軸にとったグラフのこと。
⇒面積が距離を表していることを暗記しよう!
⇒傾きが加速度を表していることを暗記しよう!
速度v × 時間t =距離 より、
たて×よこ(y軸とx軸を掛け算)の面積が、ちょうど移動距離を表現しているグラフとなっている。
速度の合成
速度 Va で運動している物体 A の上で,Vb で物体 B が運動する場合,
静止した人から見ると,物体 B の速度は、Va+Vbとなる。
例題
東向きを正方向として,
水の流れが東向きに 10m/s の川で,船が東向きに 2m/s( 静水に対する速度 ) で運動する場合,
静止した人から見て,物体 の速さはいくらか。
解答表示
相対速度
*A視点
静止している人から見た物体 A の速度が Va,物体 B の速度が Vb のとき,
物体 A に対する物体 B の相対速度 Vab = Vb – Va となる。
例 Aの速度は+10、Bの速度は-20とすると、
Aに対するBの速度は、-20-10=-30 (AからするとBは-30で移動しているように見える)となる。
*ヒントの速度自体は静止している人視点、A視点からの相対速度はAが主人公。
例題
東向きを正方向として,
東向きに 5m/s で運動している物体 A と,東向きに 15m/sで運動する物体 B がある。
物体 A から見た,物体 B の速度はいくらか。
解答表示
例題2
南向きを正方向として,
南向きに 50km/h で運動している自動車から,北向きに20km/h で運動するバイクを見たとき,
バイクの速度は何 km/h か。
解答表示
加速度a(m/s2・メール毎秒毎秒)
つまり、加速度とは速度の時間変化率のこと。
*英: acceleration
式 $ 加速度= \frac{速度V}{時間t} $
*もし、傾きが0なら等速直線運動。
*加速度×時間=速度
例題
速さ 10m/s で進んでいた自動車がブレーキをかけたところ,
一様に減速して 2.0s 後に止まった。
加速度はいくらか。
解答表示
→2秒で速度-10
→1秒で速度-5
-5.0m/s2
例題2
x 軸上を初速度 15m/s で進む物体が,
-2.0m/s2 の一定の加速度で 10s 間運動すると,速度はいくらになるか。
解答表示
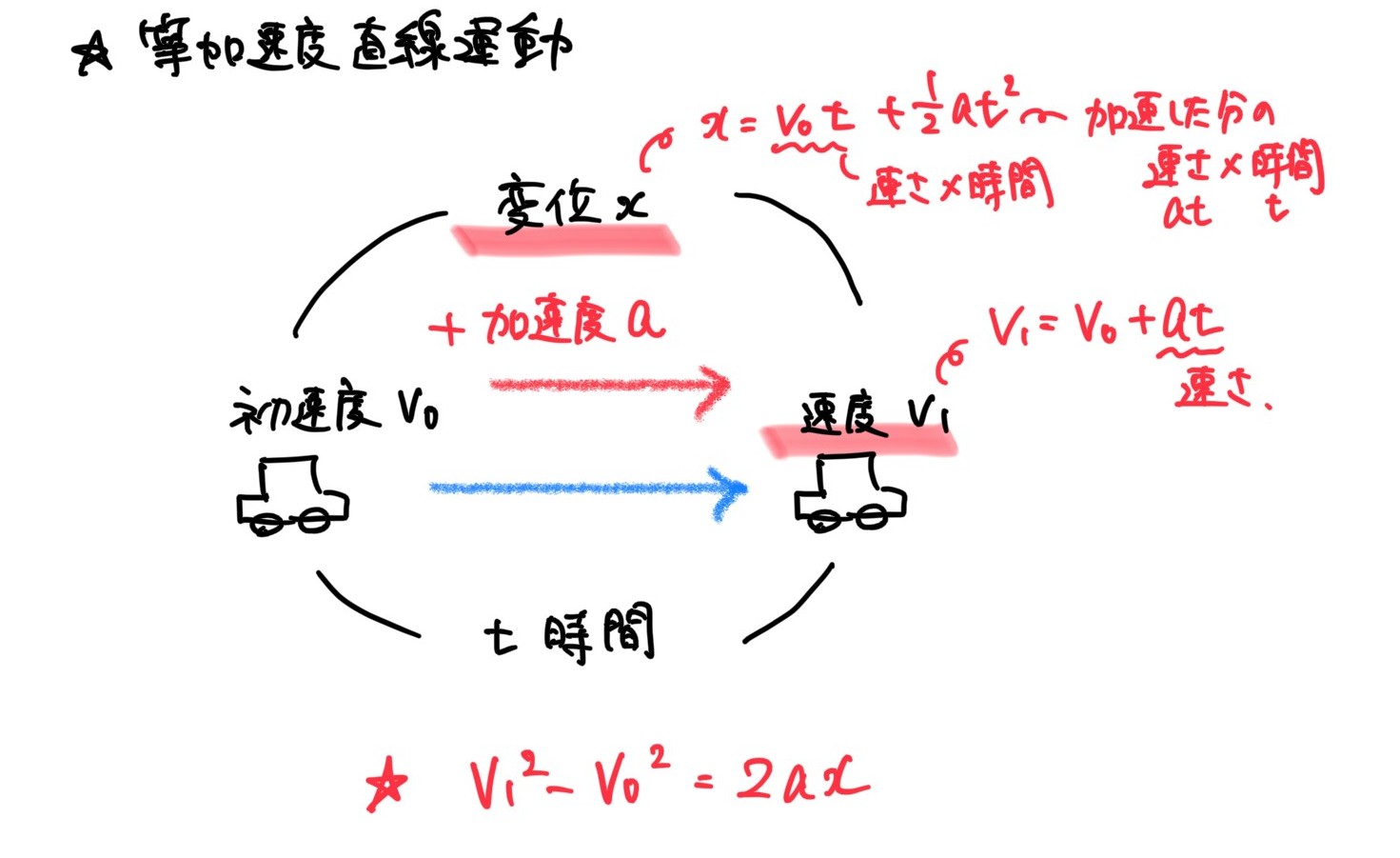
等加速度直線運動
【等加速度直線運動の公式】
初速、時間、加速度がわかれば、現在の速度や距離がわかる。
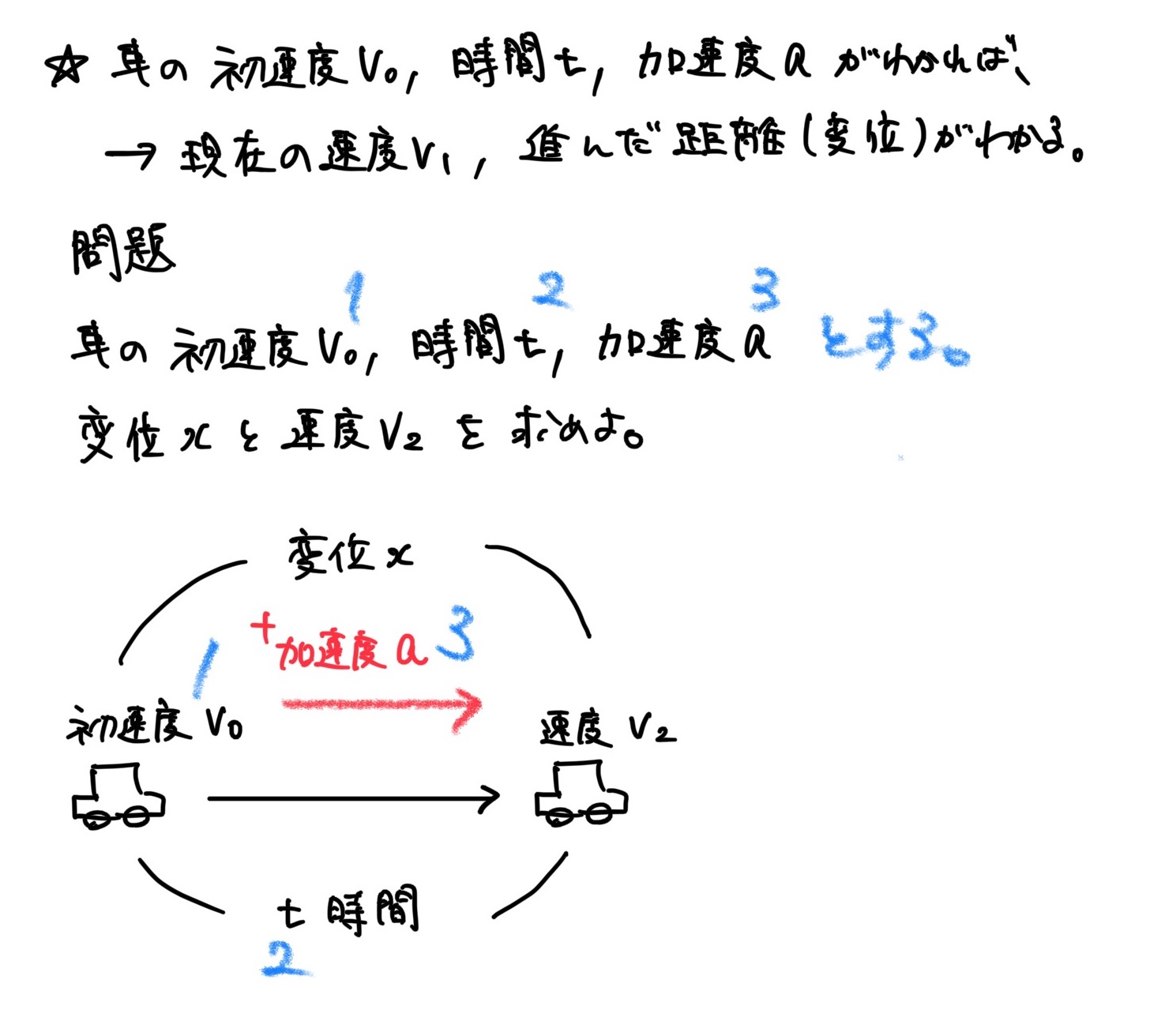
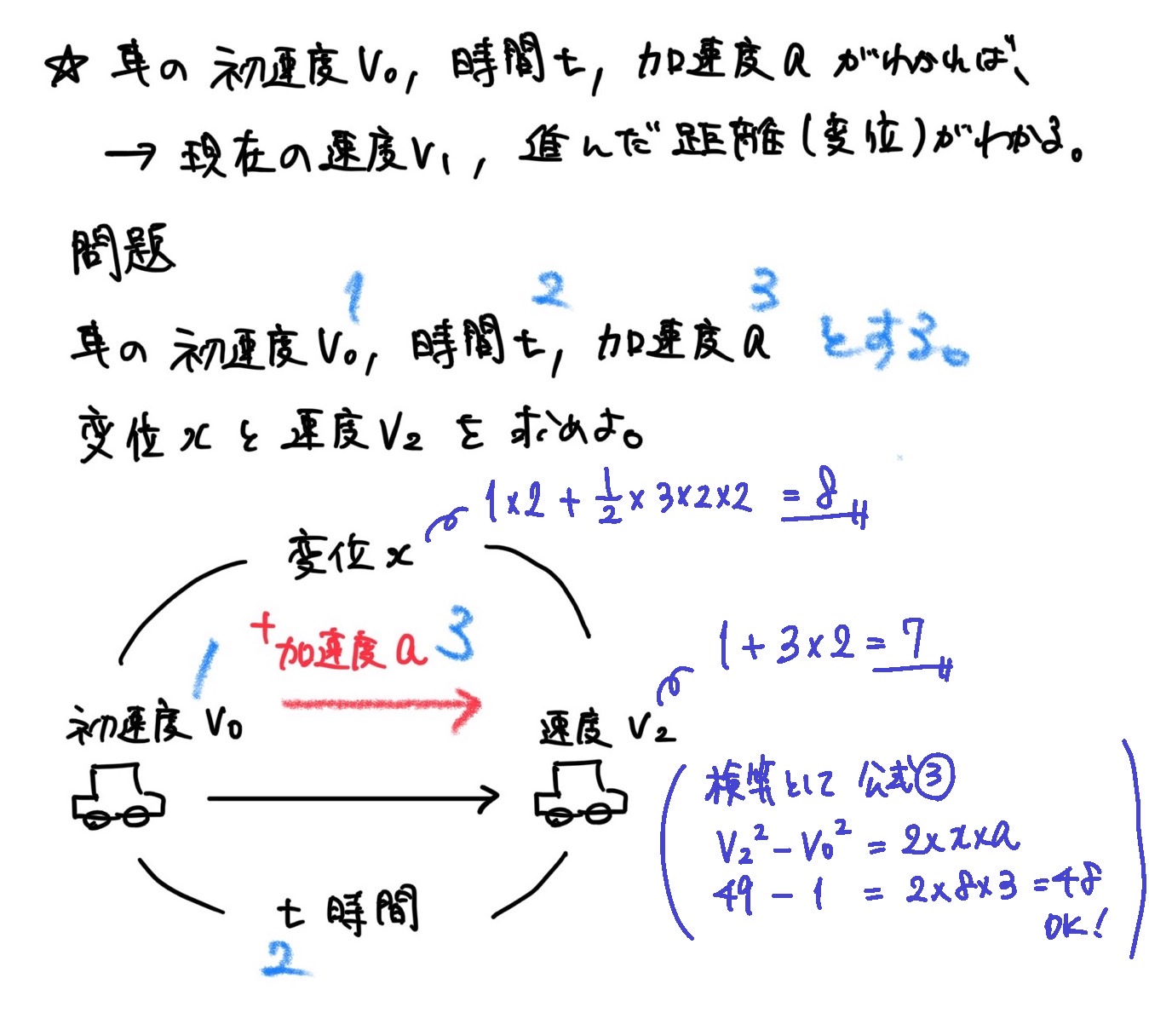
問題
図をイメージして、公式を使ってみよう。
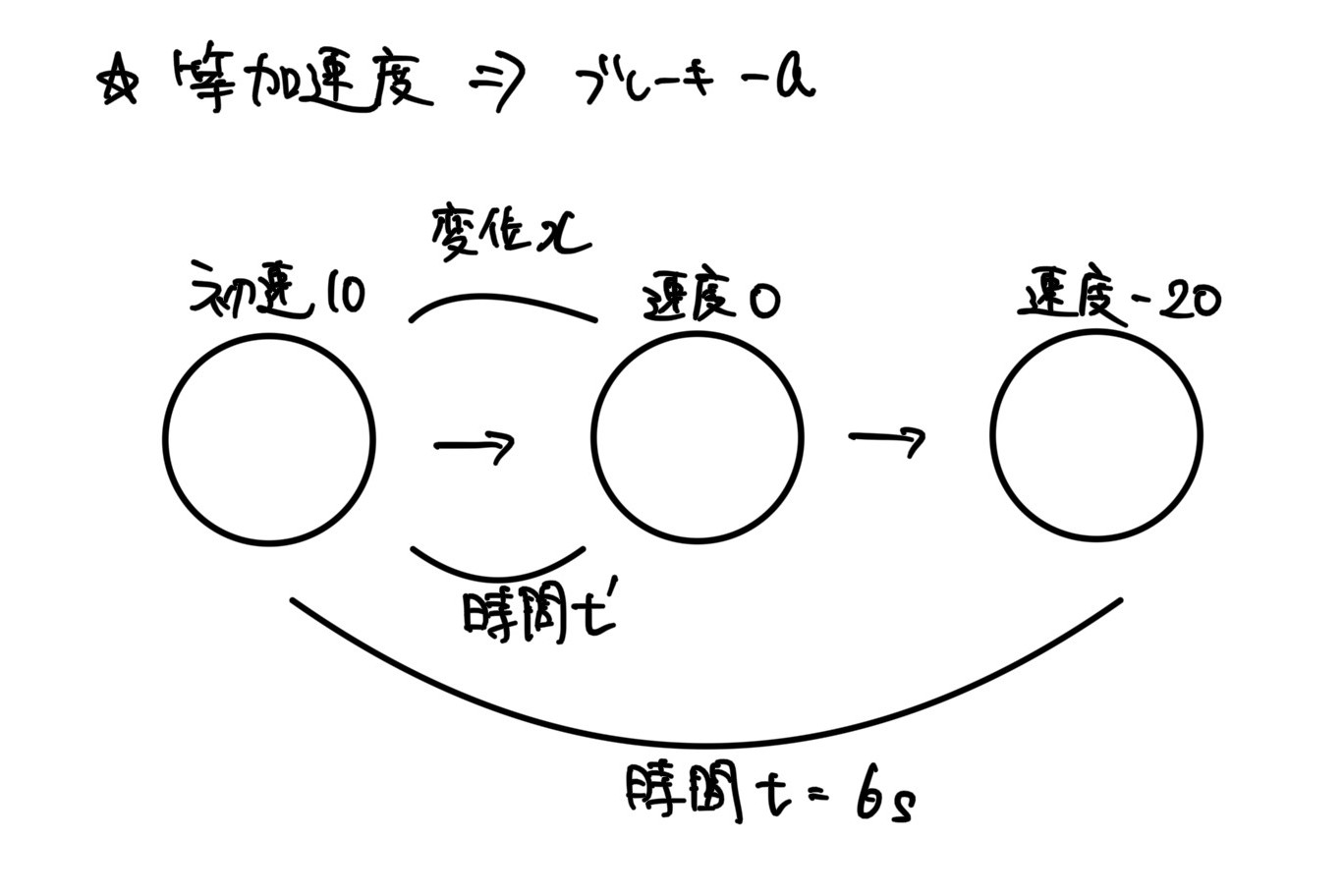
問題2
物体がはじめ速度 10m/s で運動していた。
一定の加速度をかけていったところ,加速度をかけ始めて 6.0s 後,
物体の速さは負の向きに 20m/s になった。
はじめに物体が走っていた方向を速度,加速度の正方向とする。
等加速度直線運動のグラフ(vtグラフ)
等加速度直線運動(自由落下)
★重力加速度g
自由落下のときの加速度は,大小軽重どんな物体でも一様で鉛直下向き(重力の向き)に 約 9.8m/s2 である。
【等加速度直線運動(自由落下)の公式】
等加速度直線運動の公式をそのまま使うことができる。
初速を0代入したものとなる。
加速度は重力加速度9.8を使う。
つまり、時間さえわかれば、現在の速度や距離がわかる。逆に現在の速度さえわかれば、時間がわかる。また、距離がわかれば、時間がわかる。
問題
重力加速度を 9.8m/s2 とする。
(1)物体を自由落下させた。1s 後の物体の速さと移動距離を求めよ。
(2)高さ 19.6m の屋上から物体を自由落下させた。物体は何 s 後に地面に着くか。
(3)ある高さのところから物体を自由落下させたところ,地面に着く直前の物体の速さは 19.6m/s であった。物体を放した位置は何 m の高さか。
解答表示
速さ:初速+追加速度より、0+9.8×1秒=9.8 答え9.8m/s
移動距離(速さ×時間):初速の距離+追加の距離より、0×1秒+9.8×1×1÷2=4.9m
(2)
移動距離(速さ×時間):初速の距離+追加の距離より、19.6=0×t秒+9.8×t×t÷2 この方程式を解くと、2秒後
(3)
最初と最後の速さが分かっているので、公式3が使える。
vの2乗=2×g×xより、19.6の2乗=2×9.8×x この方程式を解くと、19.6m
別解:移動距離xの公式を使っても良い。
等加速度直線運動(鉛直投げ上げ・鉛直投げ下ろし)
鉛直投げ上げは、言い換えると、上向きに初速で打ち上げ、あとは下向きの重力加速度が常にかかるという等加速度直線運動と考えることができる。
逆に
鉛直投げ下ろしは、下向きに初速で投げつけて、あとは同じ方向(下向き)に重力加速度が常にかかるという等加速度直線運動と考えることができる。
*等加速度運動の公式を,加速度 ±g(9.8m/s2) で使うだけ。
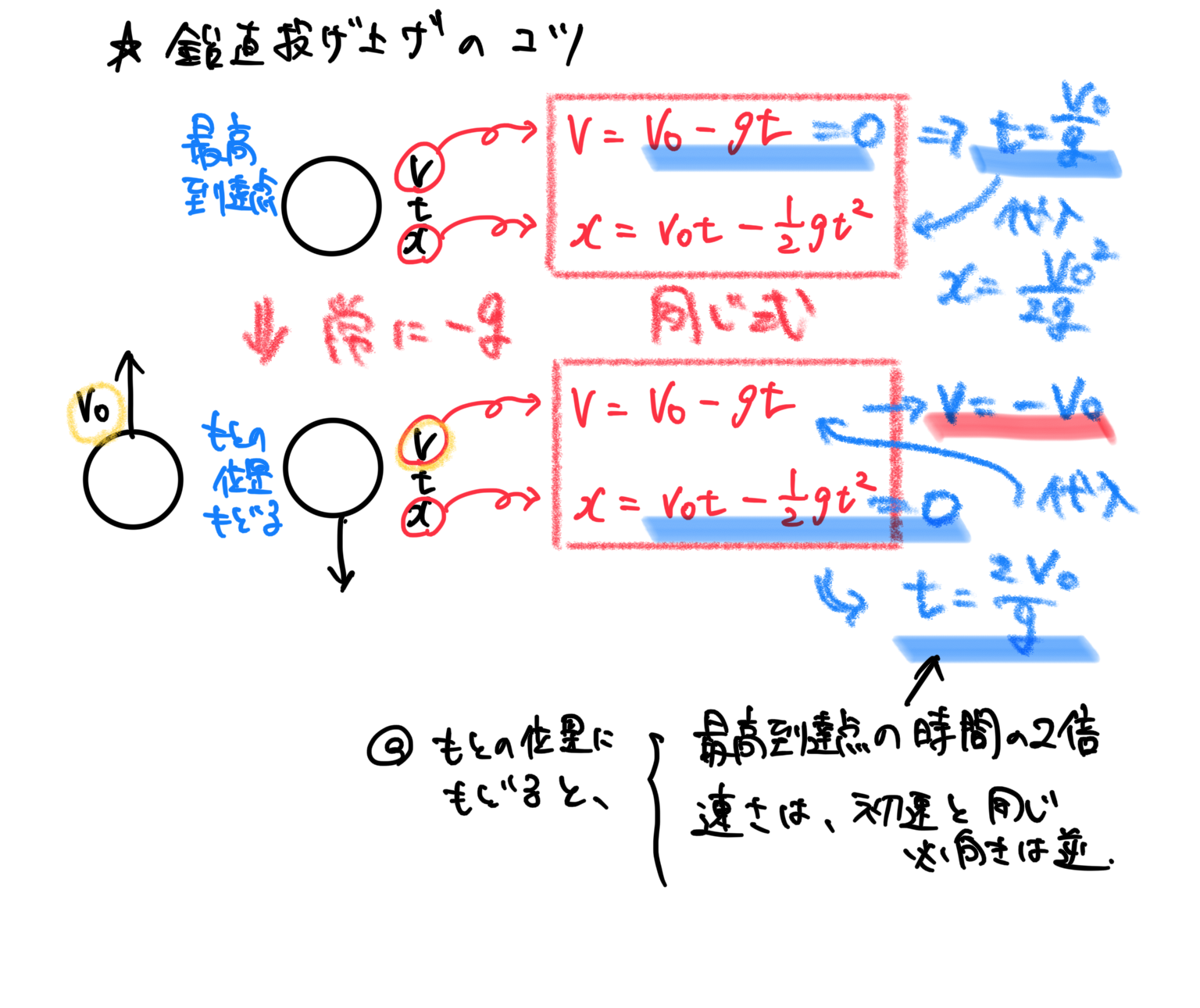
鉛直投げ上げ
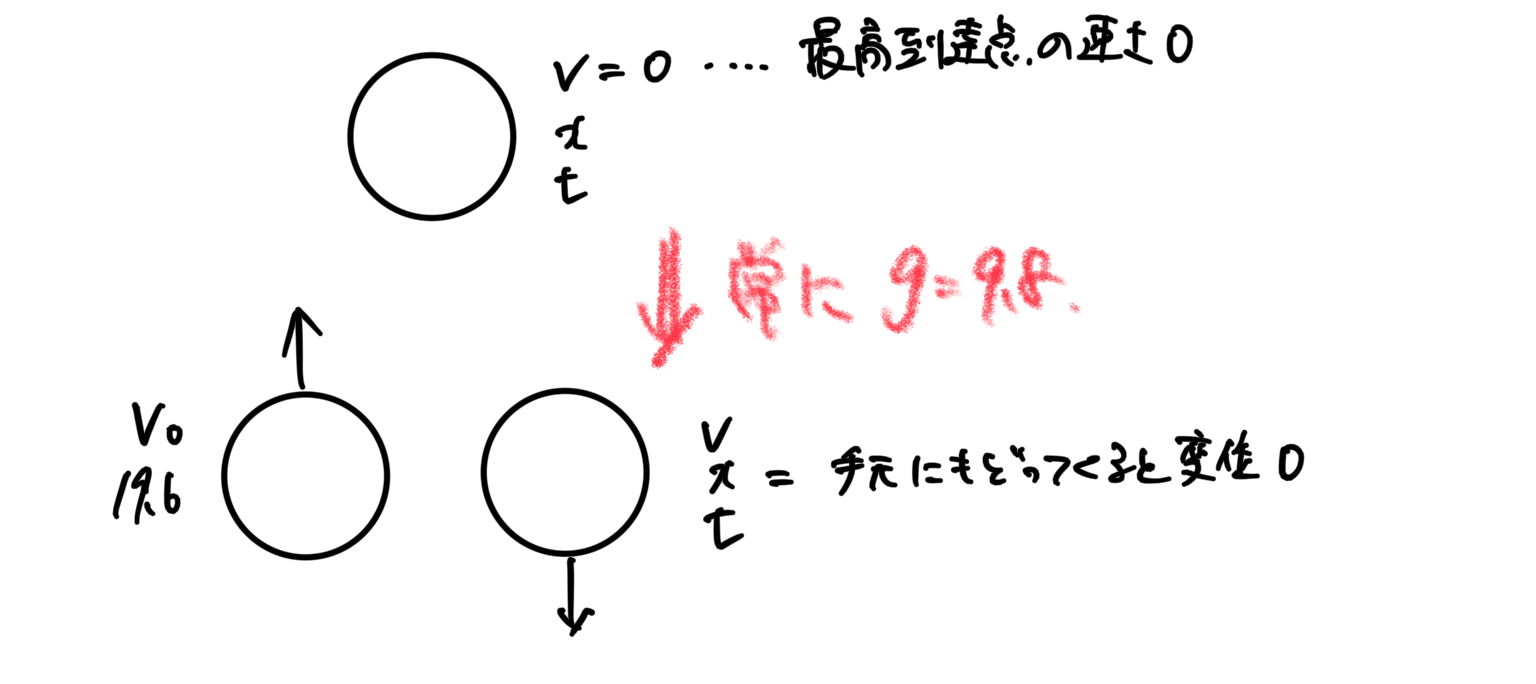
物体をある初速度で鉛直上向きに投げると,物体の速度は次第に遅くなっていき,やがて最高点で速度0となる。
その後の物体の運動は,最高点をスタート地点とする自由落下となる。
手元(最初の位置)に戻ってくると、移動距離に変化はないので、変位は0となる。
【知識】最高到達点にかかる時間をtとすると、手元に戻ってくる時間は2tとなる。つまり、上まで上がる時間=下に戻る時間。
【知識】手元に戻ってきたときの速さは、初速と同じになる。*方向は逆ベクトルだが、大きさは同じ。
このとき,終始一定の重力加速度の下での運動となっている。よって、等加速度直線運動の公式で、a = -g を代入した式を使うことができる。
最高点で折り返す前後で、式を場合分けする必要はない。
常に重力加速度がかかっているので、常に同じ式が使える。一度、式をメモして、ヒントを代入していくだけで良い。
問題
重力加速度を 9.8m/s2 とする。
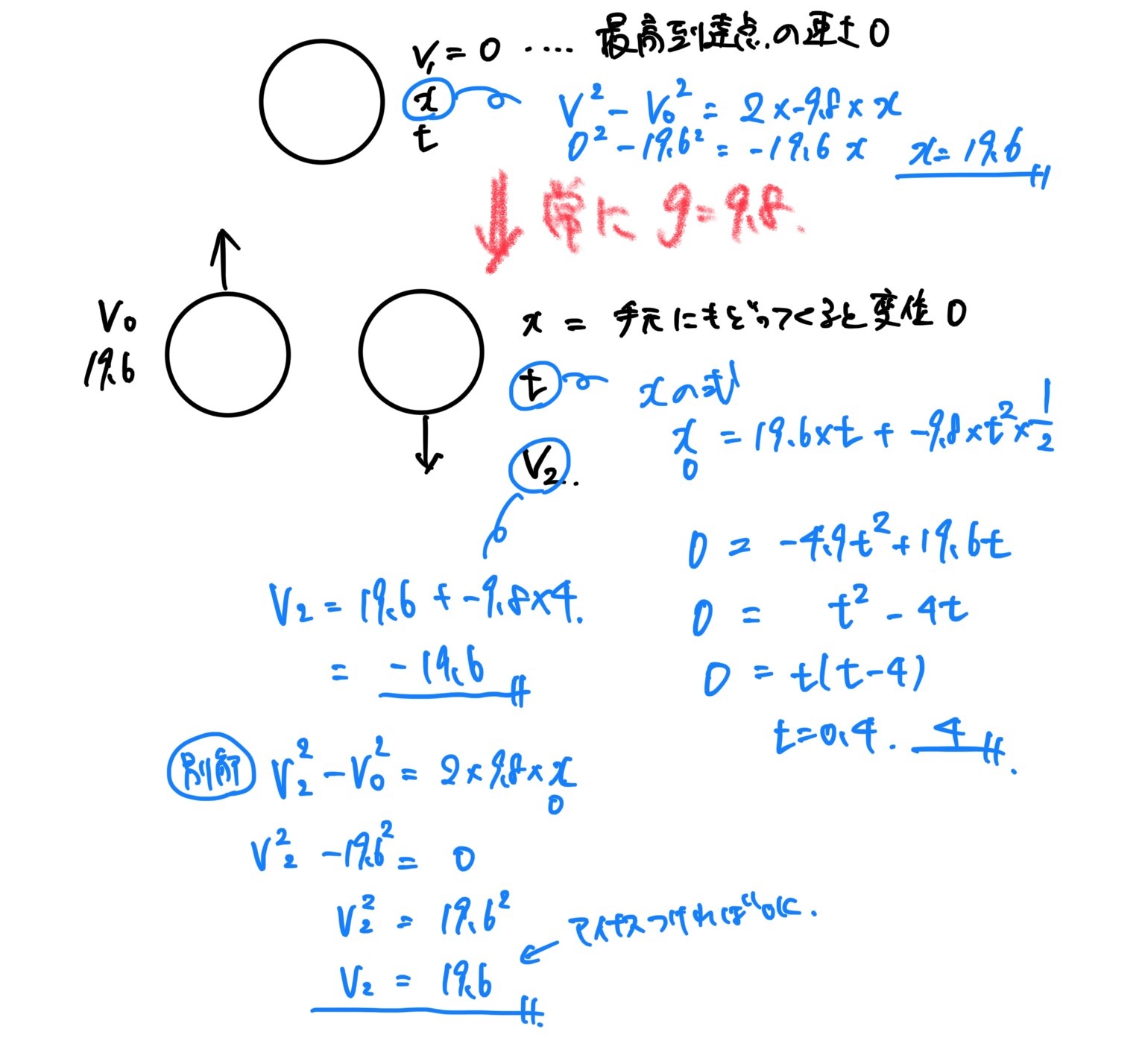
小球を初速 19.6m/s で鉛直上向きに投げた。
最高点での速さ,加速度の大きさ,高さはいくらか。
また、手元に戻ってくるまでにかかる時間と,戻ってきたときの小球の速度を求めよ。
鉛直投げ下ろし
等加速度直線運動の公式で、a = +g を代入した式を使うことができる。
問題
重力加速度を 9.8m/s2 とする。
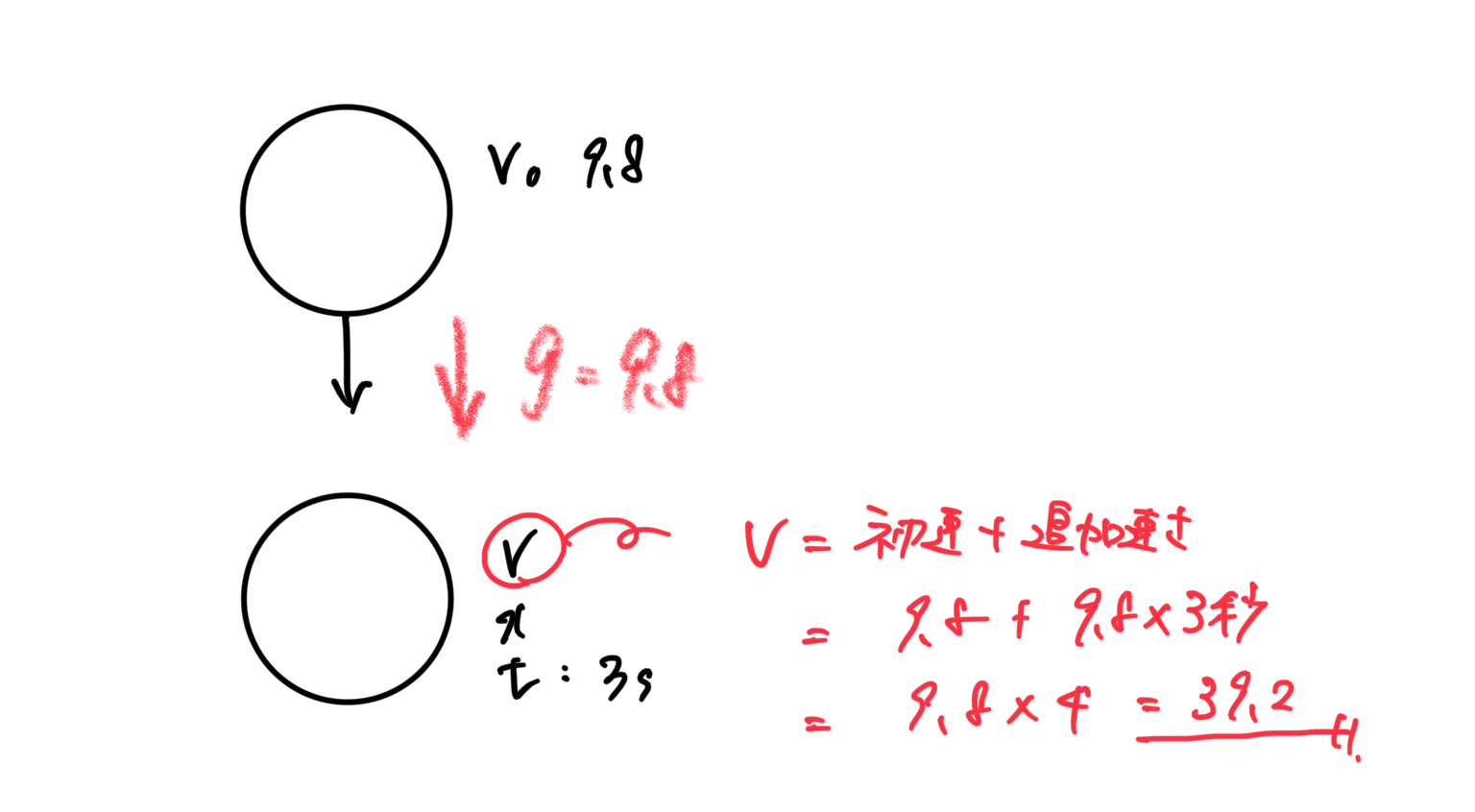
小球を初速 9.8m/s で鉛直下向きに投げた。
3s 後の小球の速さはいくらか。
テストで90点以上が取れるコツ
1、学校のワーク(問題集)をテスト1週間前までに解き終わり基本を身につける。
2、定期テスト過去問を解く。
3、入試問題(正答率20%以下)を解く。
定期テスト過去問を解くだけでも、十分な得点を狙えます。
しかし、満点を狙いたい方へ。
学校の先生によっては、100点を防ぐために、入試問題まで出題される方がいらっしゃいます。
受験ガチ勢チートでは、受験のプロが完全無料で、入試問題を丁寧にわかりやすく解説しています。
是非、チャンネル登録をお願いいたします↓↓
-120x120.jpg)
.jpg)
等速直線運動と、等加速度直線運動-1.jpg)

.jpg)
.jpg)
の公式.png)