そもそも極限とは、限りなくある値に近づくことをさす。
その値を、極限値という。
極限の種類・用語の定義(収束、極限値、無限大∞、発散、振動とは)
-993x1024.png)
【高校数学をわかりやすくまとめ・数Ⅲ】数列の極限(収束、極限値とは)
-752x1024.png)
【高校数学をわかりやすくまとめ・数Ⅲ】数列の極限(発散、無限大∞とは)
-1024x631.png)
【高校数学をわかりやすくまとめ・数Ⅲ】数列の極限(振動とは)
.jpg)
【高校数学をわかりやすくまとめ・数Ⅲ】数列の極限の種類(収束、発散、振動とは)
極限の性質
収束する場合の四則演算
-1024x567.jpg)
【高校数学をわかりやすくまとめ・数Ⅲ】数列の極限の性質(収束する場合の四則演算)
収束せずに発散する場合の四則演算
-548x1024.png)
【高校数学をわかりやすくまとめ・数Ⅲ】数列の極限の性質(収束せずに発散する場合の四則演算)
-617x1024.png)
【高校数学をわかりやすくまとめ・数Ⅲ】数列の極限の性質(不定形の計算方法)
無理式のとき-745x1024.png)
【高校数学をわかりやすくまとめ・数Ⅲ】数列の極限の性質(不定形の処理方法)無理式のとき
-1024x572.jpg)
【高校数学をわかりやすくまとめ・数Ⅲ】数列の極限の性質(はさみうちの原理)
無限等比数列とは
そもそも数列は、無限に続く数の列であるが、その中でもn番目を考えていく、というだけの話。
名前にそれほど意味はなく、あえて「無限~数列」と書いているだけである。
-1024x950.jpg)
【高校数学をわかりやすくまとめ・数Ⅲ】無限等比数列の極限(そもそも無限等比数列とは、収束条件)
-864x1024.png)
【高校数学をわかりやすくまとめ・数Ⅲ】無限等比数列の極限(不定形の処理方法のコツ)
無限級数とは
無限級数とは、無限につづく数列の和の式のこと。
.png)
【高校数学をわかりやすくまとめ・数Ⅲ】無限級数とは(無限に続く数列の和の式のこと)

【高校数学をわかりやすくまとめ・数Ⅲ】無限級数の収束条件
無限等比級数とは
無限等比級数とは、
「無限級数とは、無限につづく数列の和の式のこと」であったが、その数列が等比数列の場合のこと。
例
初項a , 公比が-1の場合、
無限等比級数は、a+-a +a+-a +a+-a +a+-a +a+-a… と無限に続く足し算であるわけだが、
答えの和が0の場合と、-aになる場合の2通り考えられるので、ある一定の値に「収束」せず、和が「0」にも「a」にも定まらない、振動している状態、つまり発散となる。
.png)
【高校数学をわかりやすくまとめ・数Ⅲ】無限等比級数とは(定義、収束条件など)
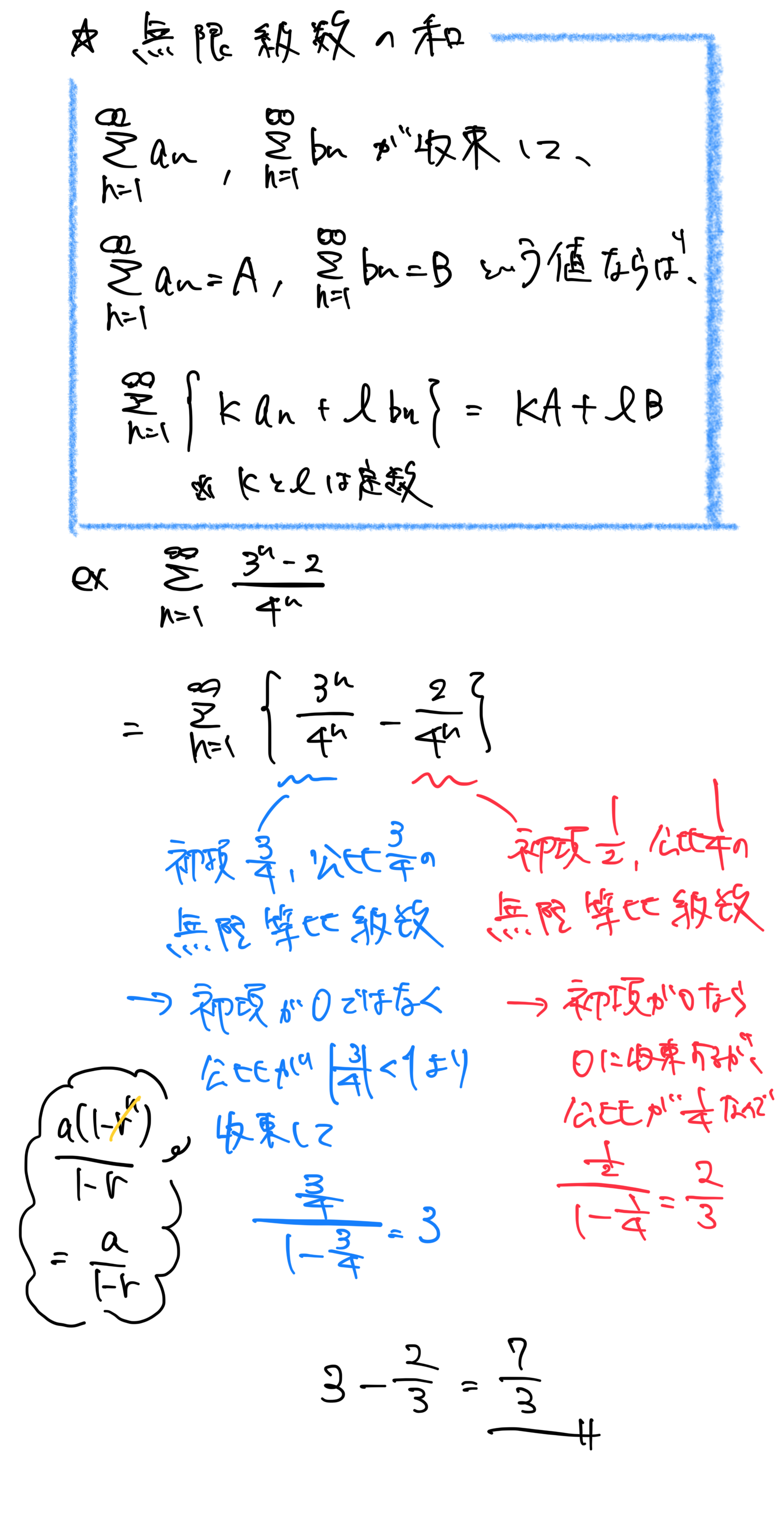
【高校数学をわかりやすくまとめ・数Ⅲ】無限級数の和
-120x120.jpg)
.jpg)
-993x1024.png)
-752x1024.png)
-1024x631.png)
.jpg)
-1024x567.jpg)
-548x1024.png)
-617x1024.png)
無理式のとき-745x1024.png)
-1024x572.jpg)
-1024x950.jpg)
-864x1024.png)
.png)

.png)
