【厳選１０問・場合の数（１）まとめ】

ディスプレイ

場合の数（１）まとめ WEB問題

単元名：規則正しい数え方、樹形図、図形の並べ方

【0 3 5 5 7 】の5まいのカードがあります。このうち3まいのカードをならべて3けたの整数を作ります。
大きい方からかぞえて5番目の整数はいくつですか。

大きい方からなので
755
753
750
735
（735）…同じなので、数えない。
730

よって、730

【0 3 5 5 7 】の5まいのカードがあります。このうち3まいのカードをならべて3けたの整数を作ります。
５の倍数は全部で何通りできますか。

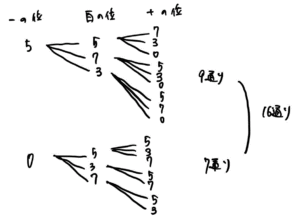
【0 1 3 7 9 】の5まいのカードのうち3まいを使って3けたの整数を作ります。
全部で何通り作れますか。

百の位は、1379の４通り
十の位は、百の位で１つ数字を使っているので、残りの４通り
一の位は、残りの３通り

よって、４×４×３＝48

【0 2 4 5 7 】の5まいのカードのうち3まいを使って3けたの整数を作ります。
偶数は何通り作れますか。

一の位が０の場合（一の位は１通り）
百の位は４通り
十の位は３通り　よって、1×4×3＝12

一の位が2か4の場合（一の位は２通り）
百の位は一の位で使った数字と0以外の３通り
十の位は残りの3通り　よって、2×3×3＝18

合わせて30通り

【A A B B C 】の5枚のカードがあります。この5枚のカードを横一列にならべます。
Aのカードがとなりどうしになり、Bのカードがとなりどうしになるならべ方は何通りありますか。

隣に並ぶパターンは、１つのセットとして考える。
つまり、A’ B’ C の３カードの並べ方を考えればよいので、３！＝６通り　＊セットの中のAAやBBは逆にしても同じ。

5人かけのベンチがあります。このべンチに A B C D E の5人がならんですわります。
5人のすわり方は全部で何通りありますか。

５！＝５×４×３×２×１＝１２０
＊５！の１２０は良く出てくるので暗記

5人かけのベンチがあります。このべンチに A B C D E の5人がならんですわります。
A B C の３人が１人おきにならぶようなすわり方は何通りありますか。

「５人いて、A B C の３人が１人おきにならぶようなすわり方」と言われたら、イメージするとこの形しかない→【A 〇 B 〇 C】
まず、ABCの順列は、３！＝３×２×１＝６通り
〇の順列は（D E）（E D）の２通りしかない。＊２！＝２×１＝２

よって、６×２＝１２

5人かけのベンチがあります。このべンチに A B C D E の5人がならんですわります。
AとBがとなりどうしになるようなすわり方は何通りありますか。

となりどうしパターンは、セットにして考える。
よって、A’ C D Eの４人の順列を考えると、４！＝４×３×２×１＝24
さらに、セットの中は（A B）（B A）の並びがあるので、２通り

24×2＝48

図のようなテーブル席に父,母,兄.私,妹のあわせて5人がすわります。
父と母が向かい合ってすわるとき、5人のすわり方は何通りありますか。

「父と母が向かい合ってすわる」場合は、アエ　か　イオ　の２通り。

アエの場合
残りのイウオに子供３人を並ばせるので、３！＝３×２＝6
さらに（ア母　エ父）（ア父　エ母）の２通り
よって、6×2＝12

イオの場合も同じ12通り

よって、24通り

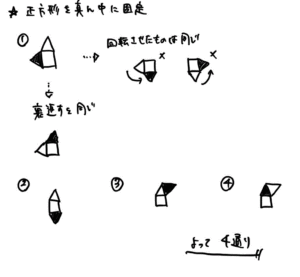
同じ大きさの正三角形のかたちをした白と黒のタイル1まいずつと、正方形の白いタイルが1まいあります。
この3まいのタイルを、辺と辺がぴったり重なるようにならべて模様をつくります。
このとき,ならべ方は全部で何通りありますか。
ただし回転したり、うら返したりして同じ図形になるならべ方は.同じものとします。

回転や裏返しを考えるのは「円順列」や「じゅず順列」という分野で、固定して考えて解くと重複なくうまく数えることができる。

円順列とじゅず順列

学習スケジュール（四ツ谷大塚、日能研）

詳しくはこちらにまとめきましたのでご参照ください。
【中学受験・小４】算数のカリキュラム・スケジュールまとめ・単元・目次一覧《日能研、四谷大塚》

受験ガチ勢チートでは、受験のプロが完全無料で、入試問題を丁寧にわかりやすく解説しています。
是非、チャンネル登録をお願いいたします↓↓

【Youtube】受験ガチ勢チート