2023年の高校２年生、新課程により数Ｃの内容となりました。
ベクトルと有向線分の違い《位置があるかどうか》
ベクトルの大きさの計算の工夫《くくる》
すべての平面ベクトルは２つのベクトルによって表現できるが、その条件は？
三角比（90°-θ、90°＋θ、180°-θ、180°＋θの覚え方）
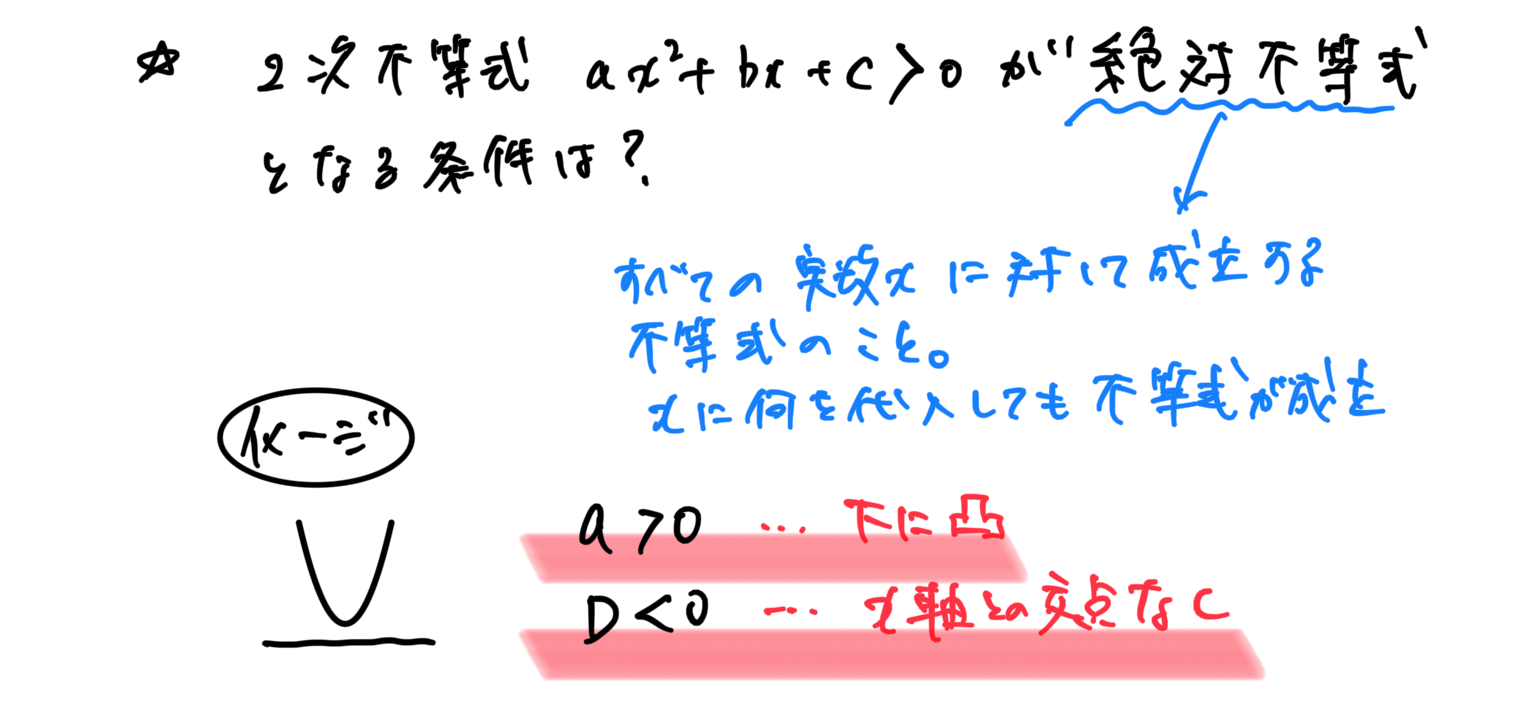
二次不等式が絶対不等式となる条件
三角形の面積の求め方４つ（三角比、ベクトルの大きさと内積、ベクトルの成分、ヘロン）
三角形の２辺とその内積がわかっているときの面積の出し方
ベクトルの内積の定義
ベクトルの不等式の証明（大きさの証明）で使いたいこと
ベクトルの大きさの２乗でわかること
内積の範囲を求める問題
ベクトルで解くか、三角関数で解くか
ベクトルの等式と三角形の面積比
点の一致の証明方法（ベクトル）
重心の位置ベクトル（公式）
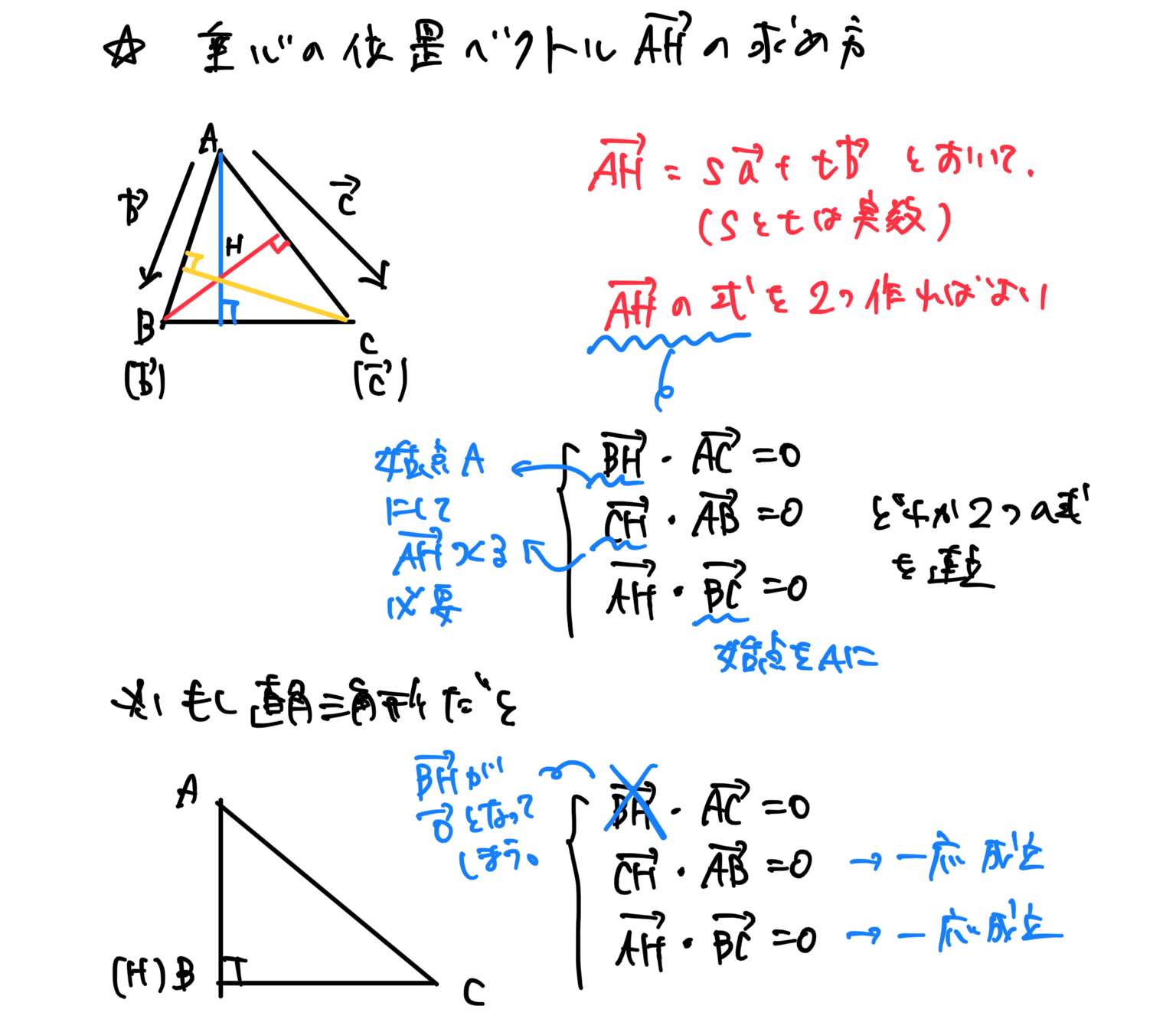
重心の位置ベクトル
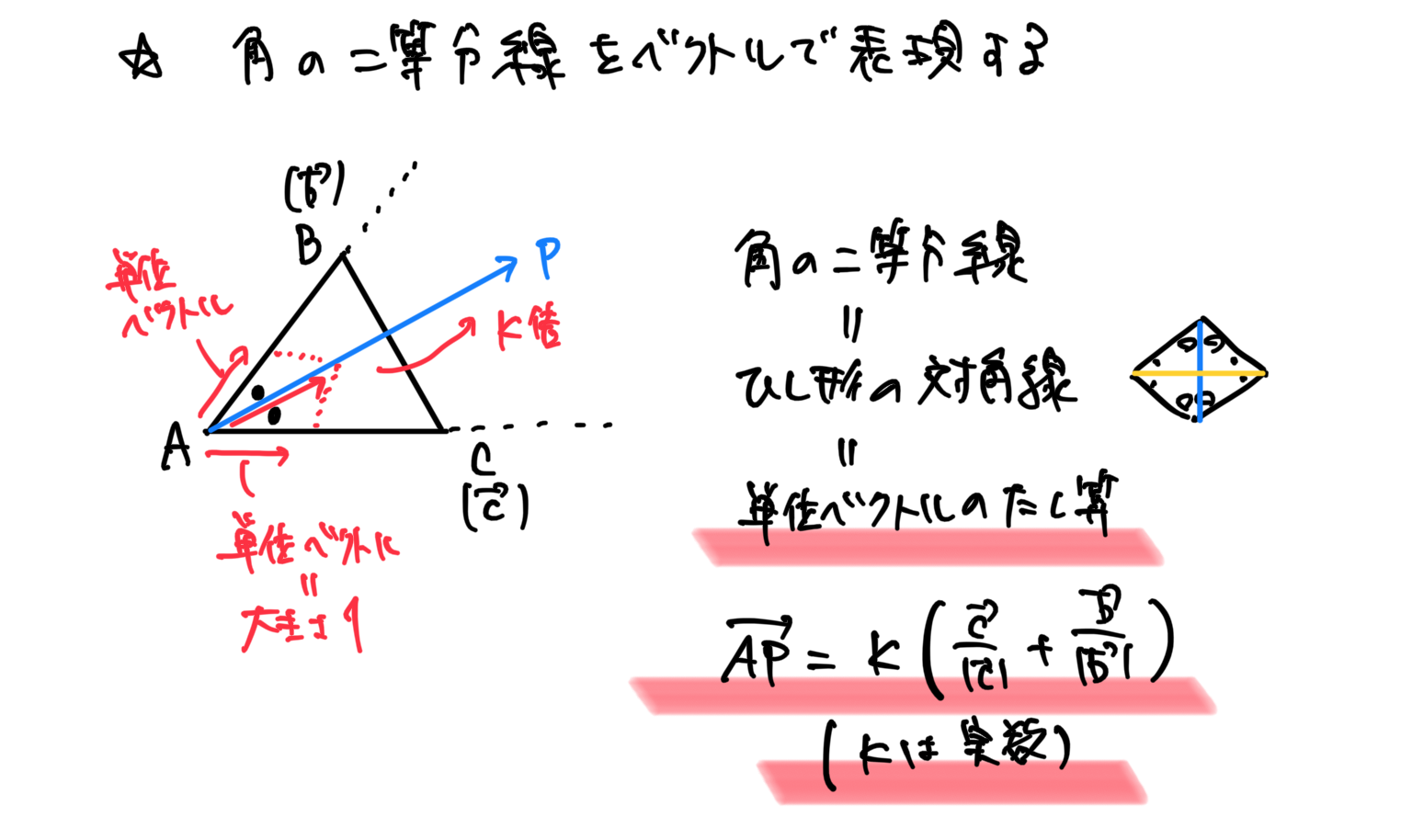
角の二等分線をベクトルで表現する
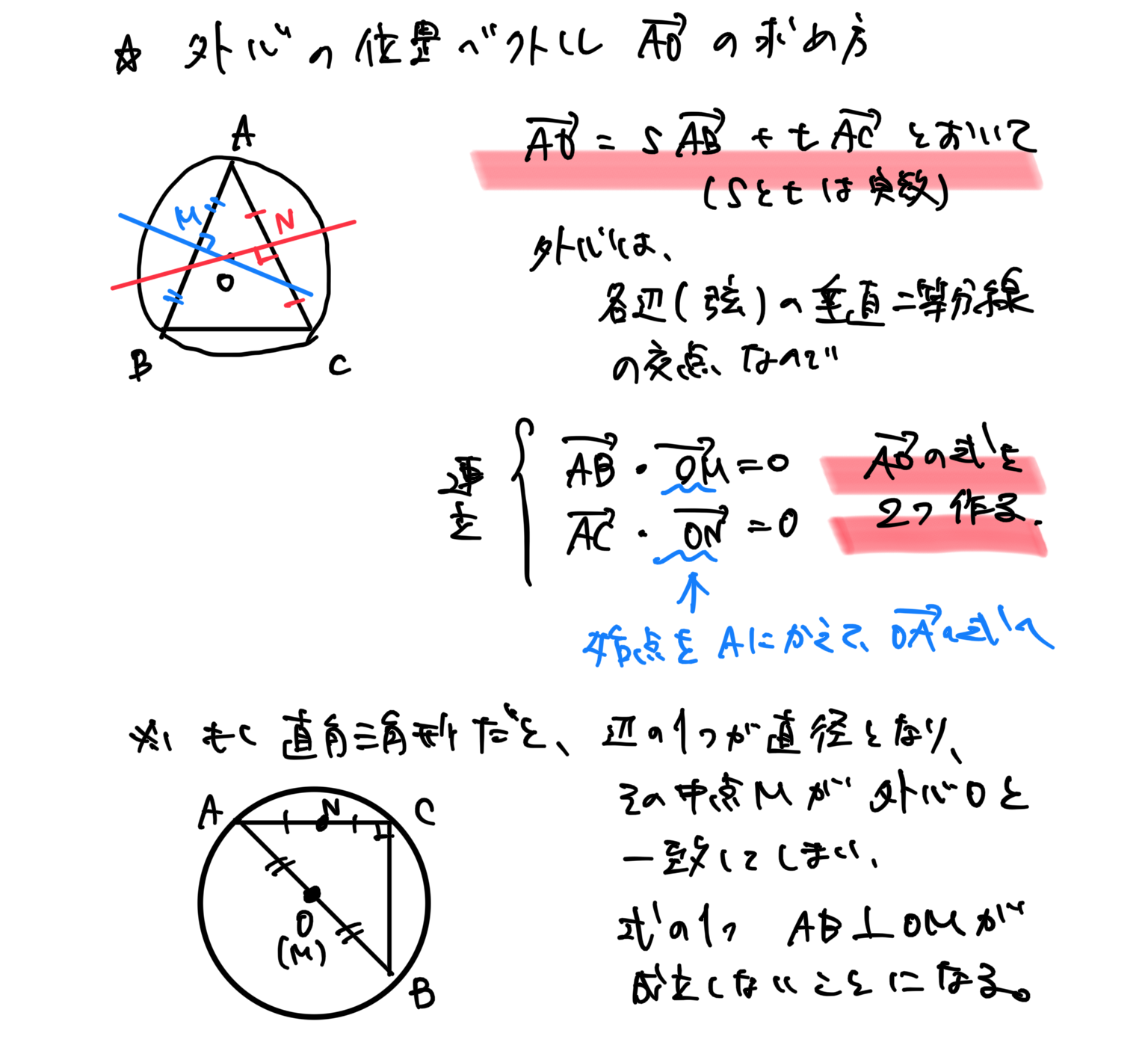
外心の位置ベクトル