【大学入試】化学《気体》重要語句と典型問題まとめ・総チェック

【大学入試】化学～目次一覧～

第1編 物質の状態
粒子の結合と結晶の構造
物質の状態変化
気体　⇒現在はここのページ
溶液

第2編 物質の変化
化学反応とエネルギー
電池と電気分解
化学反応の速さとしくみ
化学平衡

第3編 無機物質
非金属元素
金属元素Ⅰ 典型元素
金属元素Ⅱ 遷移元素

第4編 有機化合物
有機化合物の分類と分析
脂肪族炭化水素
アルコールと関連化合物
芳香族化合物

第5編 高分子化合物
天然高分子化合物
合成高分子化合物

計17章ほど

【大学入試】化学《気体》重要語句と典型問題まとめ・総チェック

計算問題における「気体」の考え方

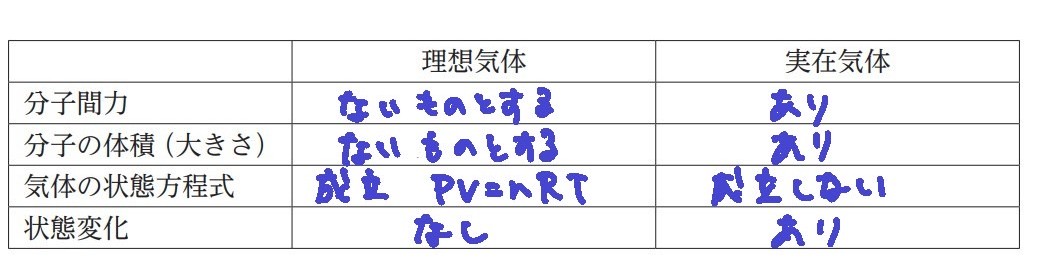
①分子間で引き合う、分子間力は無いものとして考える
分子間の引力よりも、熱運動による力の方が強すぎるため。

②分子自体の体積(大きさ)は無いものとして考える
分子自体の体積よりも、気体の体積（気体が入っている容器の体積）が大きすぎるため。

気体の圧力とは

★気体の圧力とは
気体分子が壁にぶつかる力(単位面積当たり)をさす。

★圧力の単位
①パスカル（Pa）…標準大気圧1.013 × 105Pa
②ミリメール水銀柱（mmHg）…標準大気圧760mmHg
※水銀で満たした液体の中に、容器を入れ、その中で立てると、標準大気圧と水銀柱760mmの高さになるということ。

③アトム（atm）…標準大気圧を 1atm とする。

気体の体積、気体の温度とは

★気体の体積 V
分子自体の体積ではなく、気体分子が自由に動き回れる空間の広さ（気体が入っている容器の体積）をさす。

★温度 T
絶対温度(K)= セルシウス温度(°C)+ 273
＊化学では、いつもの「～度」ではなく、「～ ケルビン k 」を使うこと。

気体の法則

P：圧力
V：体積
T：絶対温度（セルシウス温度＋273）

これら３つの関係が、
ボイルの法則：VとPは反比例
シャルルの法則：VとTは比例
となることを気体の法則という。

これらを式にしたものが、
$ \frac{PV}{T} = \frac{P’V’}{T’} $

【高校化学】ボイルの法則、シャルルの法則、どっち？

気体の状態方程式とは

そもそも圧力は、気体分子が壁にぶつかる力のことをいうため、
→圧力は、分子の運動エネルギー、つまり温度（K）に比例する。
→圧力は、分子の数（mol）、つまり単位体積あたりの分子の数（mol/L）に比例する。

※なぜ分子の数を「単位体積あたり」で考える必要があるか？
大きい容器に2粒であっても、とても小さい容器に1粒であれば、単純に2:1ではないから

よって、
圧力P＝温度T（K）✖️単位体積あたりの分子数n/V（mol/L）✖️気体定数R
→分母（V）を払って変形した式で覚えよう！

PV＝n R T をさらに変形していく。
変形で使う単位は、
Ｗ（質量ｇ）
Ｍ（分子量）＊分子量：molecular weight
ｄ（密度）＊密度：density

まずは、ｎ（物質量）＝Ｗ（質量ｇ）÷ Ｍ（分子量）より、
PV＝W/M RT と変形できる。

次にｄ（密度）＝質量ｗ÷体積Ｖより、
PV＝W/M ・RT
P＝W/M ・RT /V
P＝ｄ/M ・RT
1/P＝M /R /T /d
RTd/P =M

【高校化学】状態方程式

気体の分子量測定実験（デュマ法）

気体の分子量測定実験（デュマ法）とは
ピクノメーター（メスフラスコに「小さな穴の開いた蓋」をしたもの）を使って気体の密度を測定し，気体の分子量を求める実験のこと。

RTd/P =M より、密度ｄさえわかれば、
他の気体定数Ｒ、温度Ｔ、大気圧Ｐは一定なので、分子量Ｍがわかる。

実験内容（求めたい気体の体積と質量をはかりとり、密度を計算する。密度がわかれば分子量がわかる。）
①空気だけが入ったメスフラスコの質量をはかっておく。
②分子量を求めたい気体を液体にしたものを、メスフラスコの中にいれる。（液体の量は適当でよい）
③メスフラスコを恒温槽（温度を一定に調整できる槽）に入れて、液体を蒸発させてメスフラスコ内を満たす。…これで気体の体積がわかる。メスフラスコと同じ体積だから。
④メスフラスコを冷却して、求めたい気体を液体へ戻すと、空気がメスフラスコ内に戻ってくる。
⑤最初の空気だけが入ったメスフラスコの質量と、液体と空気が入ったメスフラスコの質量を比較すれば、液体（メスフラスコを満たしていた気体）の質量がわかる。

【化学】気体の分子量測定実験（デュマ法）計算問題の解き方

混合気体

平均分子量（見かけの分子量）とは

★平均分子量（見かけの分子量）＊そのままモルの比を使って、平均の計算をするだけ。
ある体積の空間内で、気体が混合している場合に（例：空気は窒素や酸素の混合気体）
気体Aをa mol、気体Bを b mol …として、モルの割合（モル分率）を求めて、
混合気体の分子量の平均を出すことをさす。

【化学】空気の平均分子量の求め方（モル分率など）

分体積とは

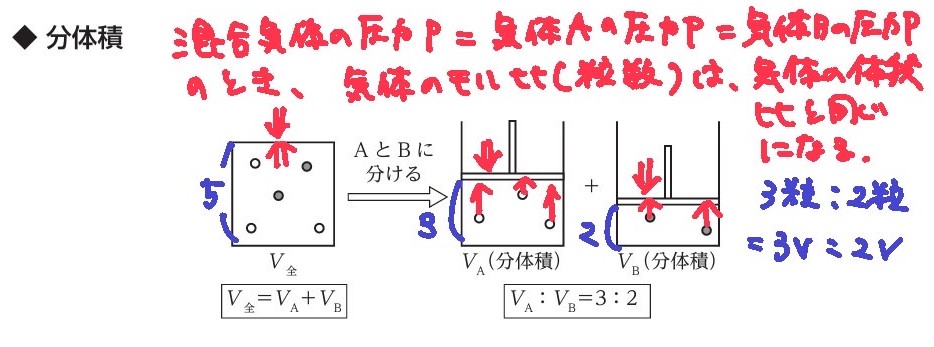
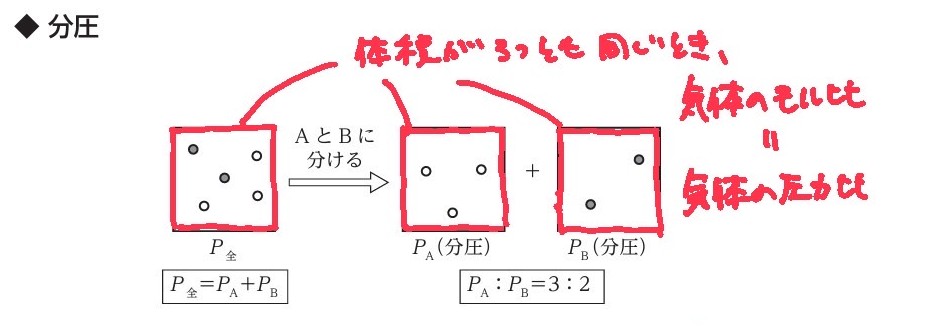
【化学】分体積とは

★分体積
混合気体の全体の体積を、それぞれの成分気体の体積に分けたものをさす。
＊言い方を変えると、それぞれの成分気体の体積を足し算をすると、混合気体の全体の体積になる。

PV＝n R T より、
圧力Pと温度Tが一定であれば（PとＴとＲは一定値となり）、
Ｖ＝ｎ「体積比＝mol比」が成立することから、
分体積の比は、モル比と同じになる。

【化学】分体積の計算問題をわかりやすく

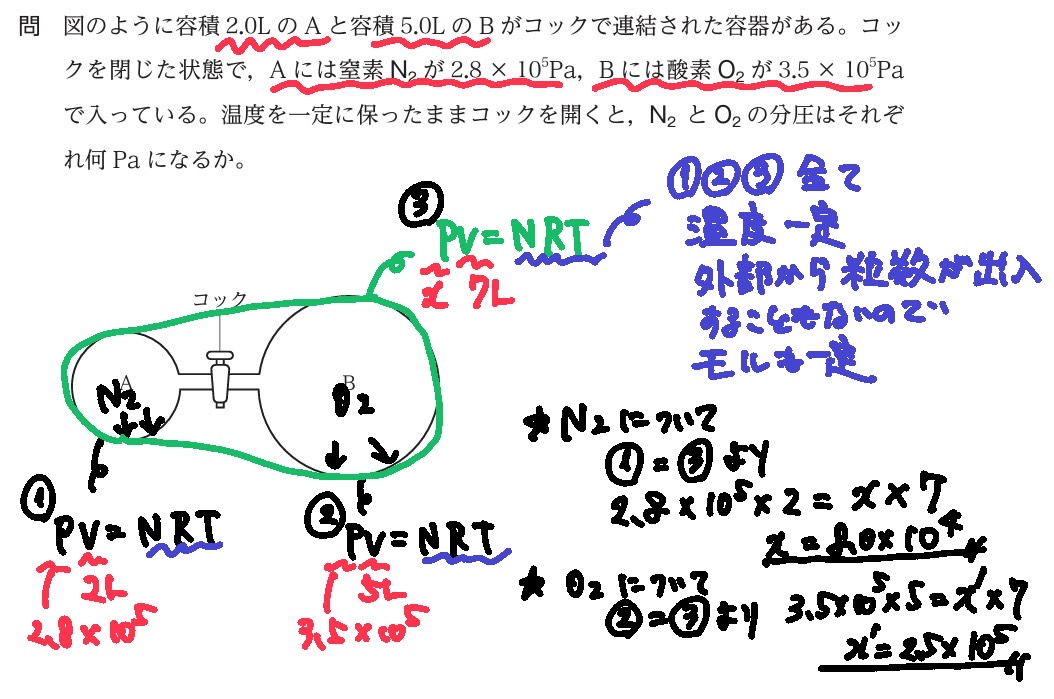
混合気体の全圧と分圧とは

【化学】分圧とは

★全圧
混合気体の示す圧力をさす。

★分圧
全圧を、それぞれの成分気体の圧力に分けたものをさす。
＊言い方を変えると、それぞれの成分気体の圧力を足し算をすると、混合気体の全体の圧力になる。

PV＝n R T より、
体積Vと温度Tが一定であれば、
P＝ｎ「分圧比＝mol比」が成立する。

【化学】分圧の計算問題をわかりやすく

【化学】分圧の計算問題②

飽和蒸気圧（Pmax）とは

《ポイント》
水、エタノール、エーテルなど、
これらが気体であるとき「蒸気」といい、圧力が高すぎると100度以上だとしても、液体になってしまうことから問題となる。

★飽和蒸気圧とは
蒸気の圧力の限界値。

また，飽和蒸気圧と温度の関係をグラフにしたものを蒸気圧曲線という。
この曲線状にあるときは、気体と液体が共存している

【高校化学】水の状態図（温度と圧力の２つの変数で、固体・液体・気体のどの状態か表した図融解曲線、蒸気圧曲線、臨界点、超臨界流体、昇華圧曲線、三重点）

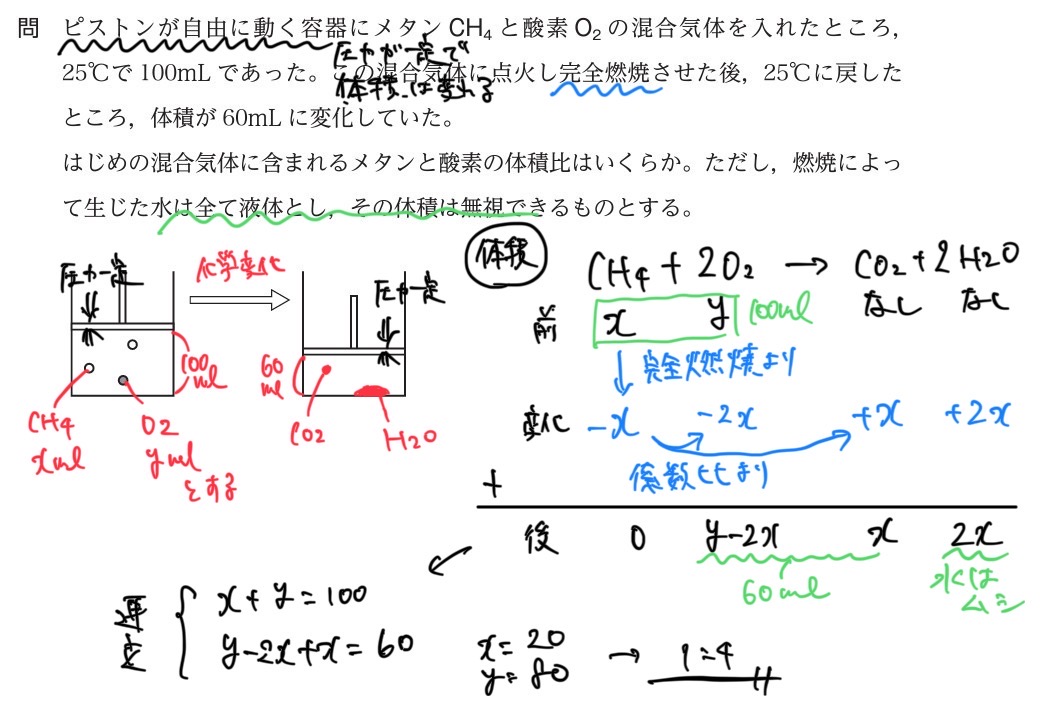
蒸気を含む気体の計算問題

【化学】飽和蒸気圧と蒸気圧曲線（状態図をピックアップしたもの）

手順
→まずは、全て気体と仮定して、普通の気体の問題と同じように圧力Pを求める。
→求めた圧力Pと、飽和水蒸気圧Pmaxを比較して、答えを修正する（気体の圧力の限界値を超えることができない）。

①P＞Pmaxの場合、気体の圧力の限界値を超えているため、一部、気体が液体に変わっている状態といえる。気体の圧力は、限界値のPmaxの値に修正する必要がある。
②P≦Pmaxの場合、気体の圧力の限界値は超えていないため、気体のみといえ、計算結果はそのまま気圧Ｐの値を使ってよい。

【化学】飽和蒸気圧の計算問題をわかりやすく

液体の水が存在しているときの気体の計算問題（水上置換）

★水上置換というヒントでわかること
・大気圧と、容器内（メスシリンダーなど）の圧力が同じ
・水上置換によって回収した気体Aと、水（水蒸気：気体B）が飽和水蒸気圧で混ざっていること
・水上置換によって回収した気体Aの体積は、気体Aと気体Bの混合気体全体の体積と同じであること。分圧が成立するから、体積は同じ。

【高校化学】液体の水が存在しているときの気体の計算問題（水上置換）

理想気体とは、実在気体とは

【高校化学】理想気体とは、実在気体とは

★体積の違いについて

分子自体の体積（高圧の状況下では、単位あたりの分子自体の大きさが無視できない）
ほんとうであれば（実在気体であれば）、分子自体の体積があるため、その分体積が大きくなる。
しかし、低圧であれば、スカスカな状態であり気体全体の体積が大きいから１粒の大きさは無視できる。よって実在気体は理想気体の状態に近づく。

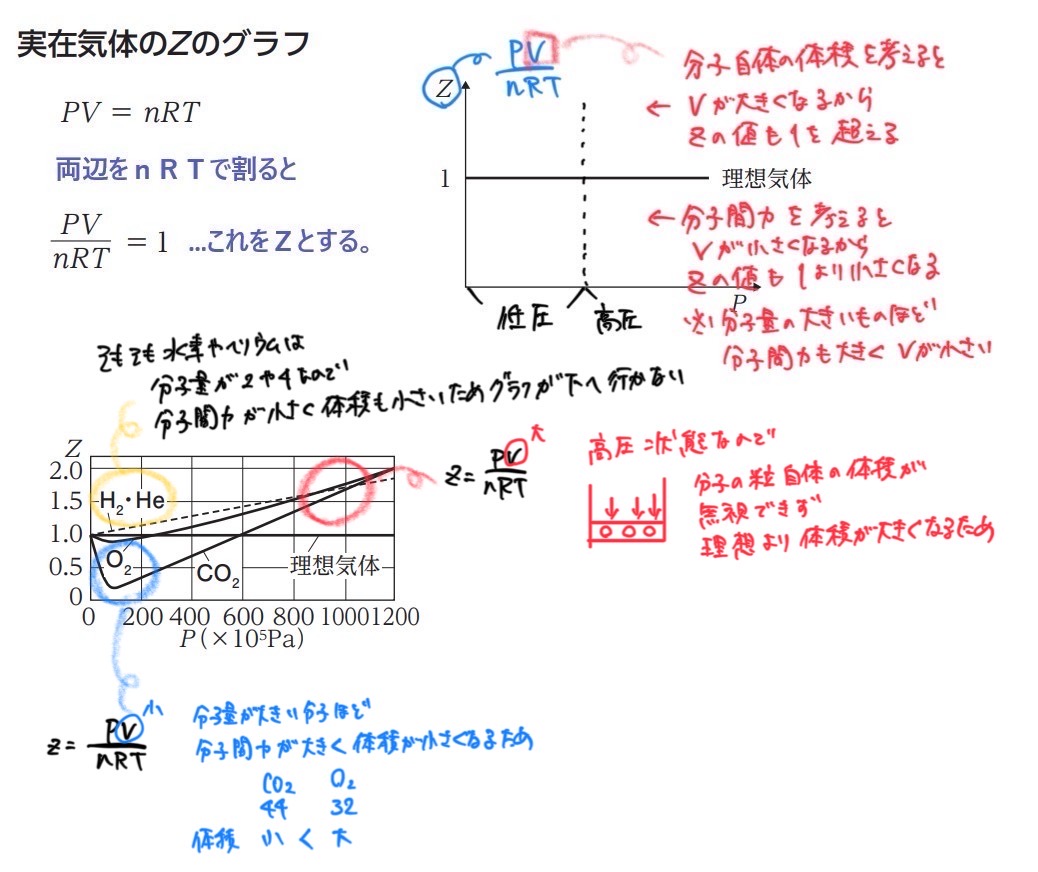
分子間力（分子量が大きい分子ほど、分子間力も大きい）
ほんとうであれば（実在気体であれば）、分子間力が働いて引きつけ合うため、体積が小さくなる。
しかし、高温にすれば、熱運動エネルギーが大きいから分子間力を無視できる。よって、実在気体は理想気体の状態に近づく。

《Zグラフ》実在気体と理想気体を、見た目で判断するためのグラフ

注意：Zグラフには、温度が考慮されていない（温度は一定）ので、高温にすれば分子間力が無視できるということは考えていない。

【高校化学】《Zグラフ》実在気体と理想気体を、見た目で判断するためのグラフ