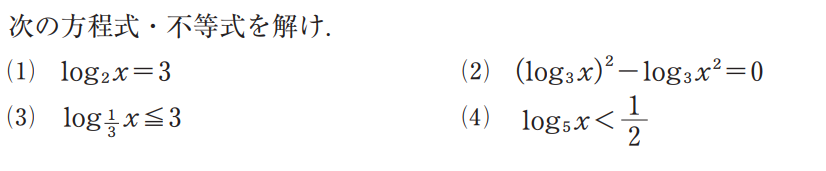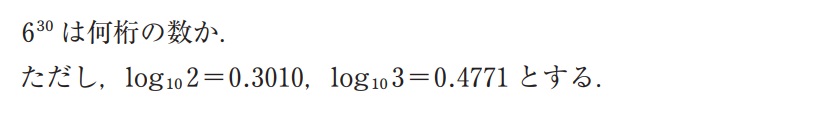0から始める大学入試数学シリーズです。プロ教師がお届けします。
教科書レベル《必ずマスターすべき典型問題》
2022年、生徒の進度に合わせて追加中!
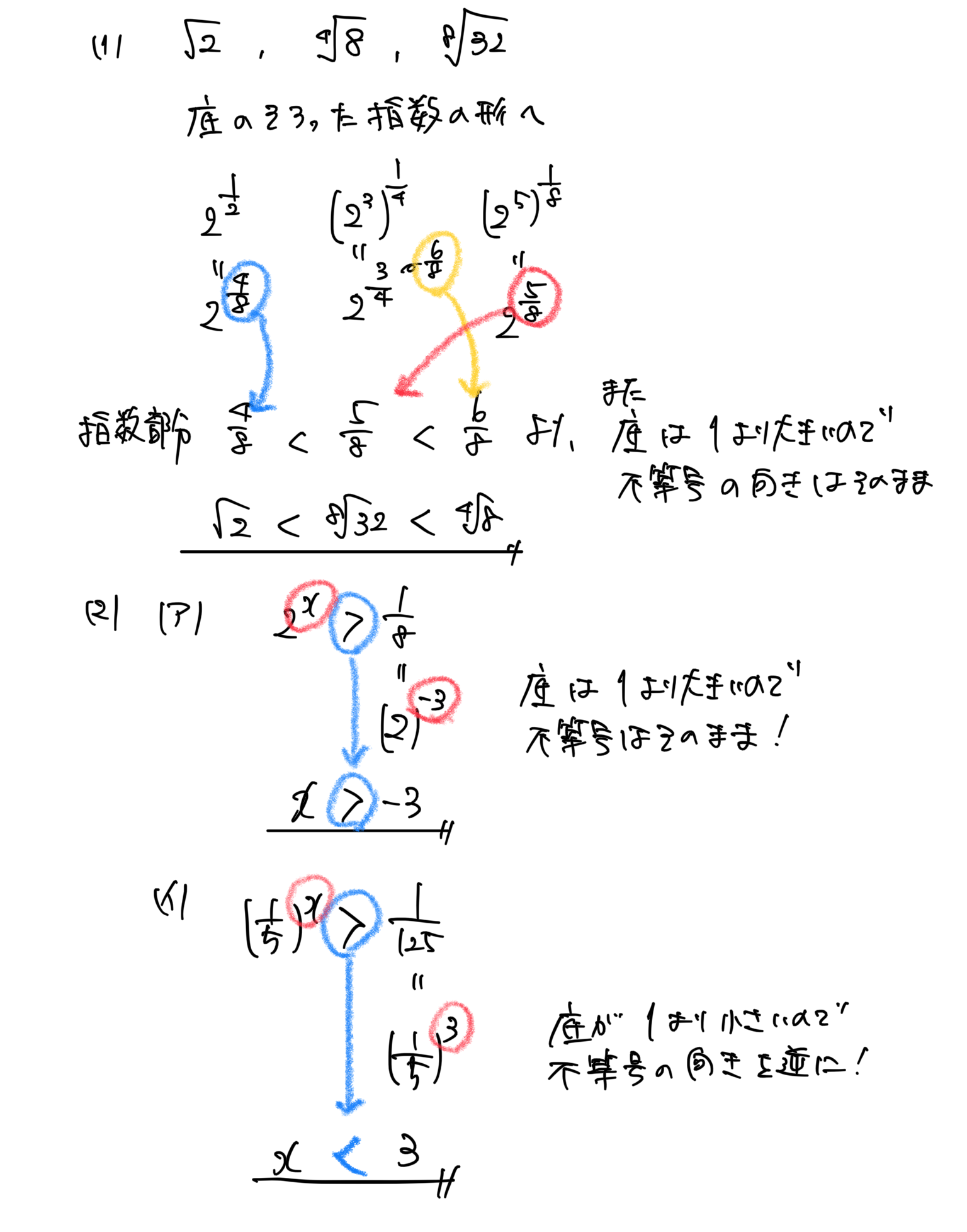
【累乗根の計算】指数の形にして計算!
一言ポイント!
★上(指数部分)で計算すると楽!
指数にすると、指数法則によって計算がしやすくなる。
素因数分解しつつ、( )して累乗根は指数へ!
★ルートの中のマイナス
累乗根の中のマイナスは、奇数乗根(3乗根など)なら外へ出ることができる!
★わり算を上に!
わり算は、かけ算に直してマイナス乗にする!
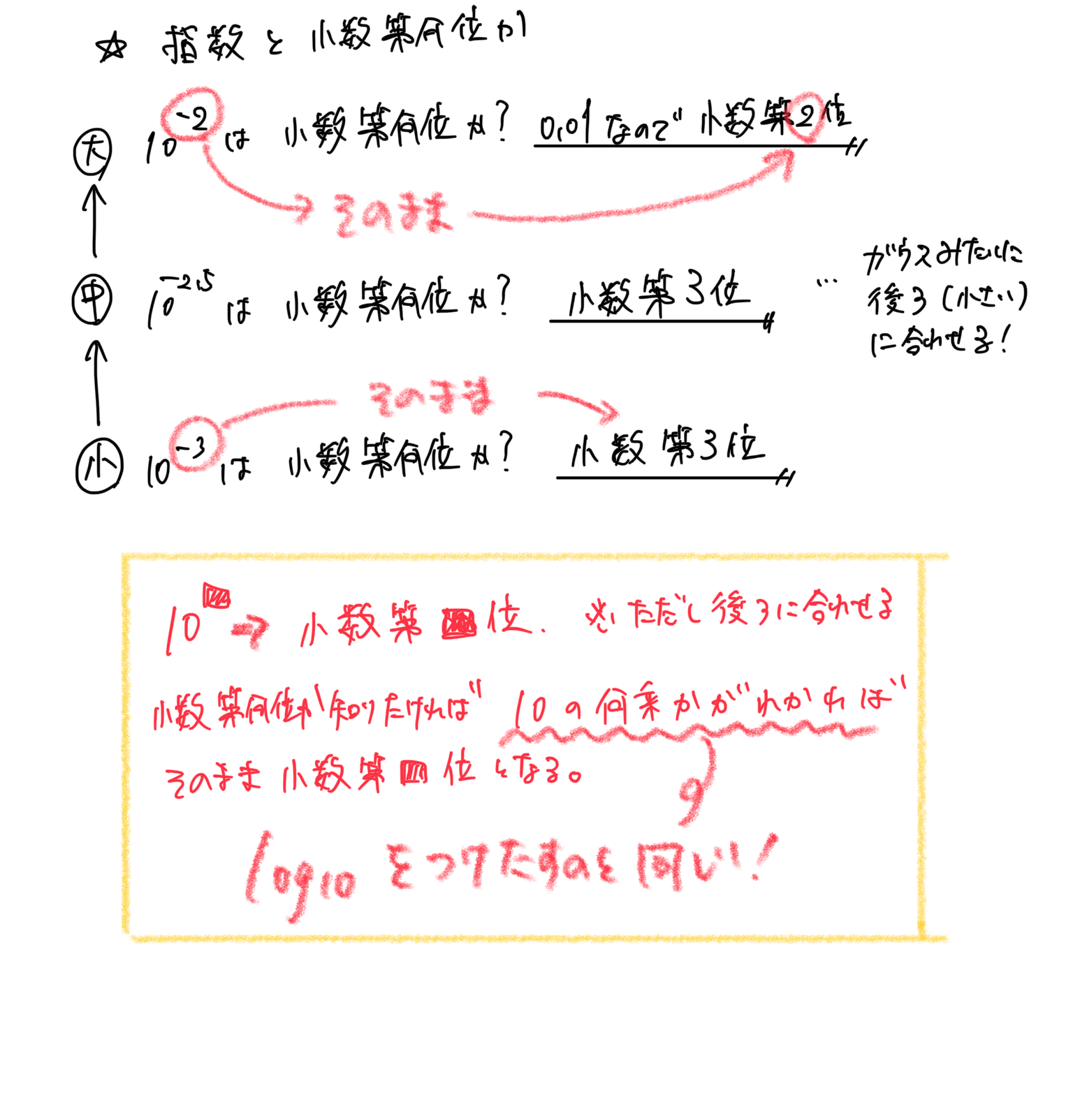
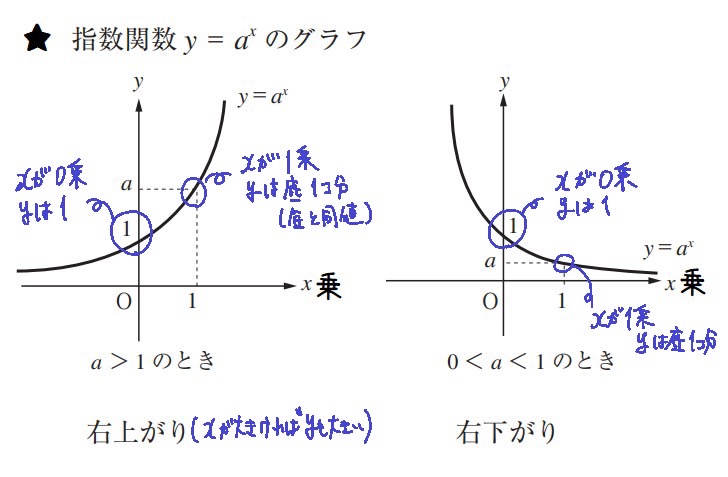
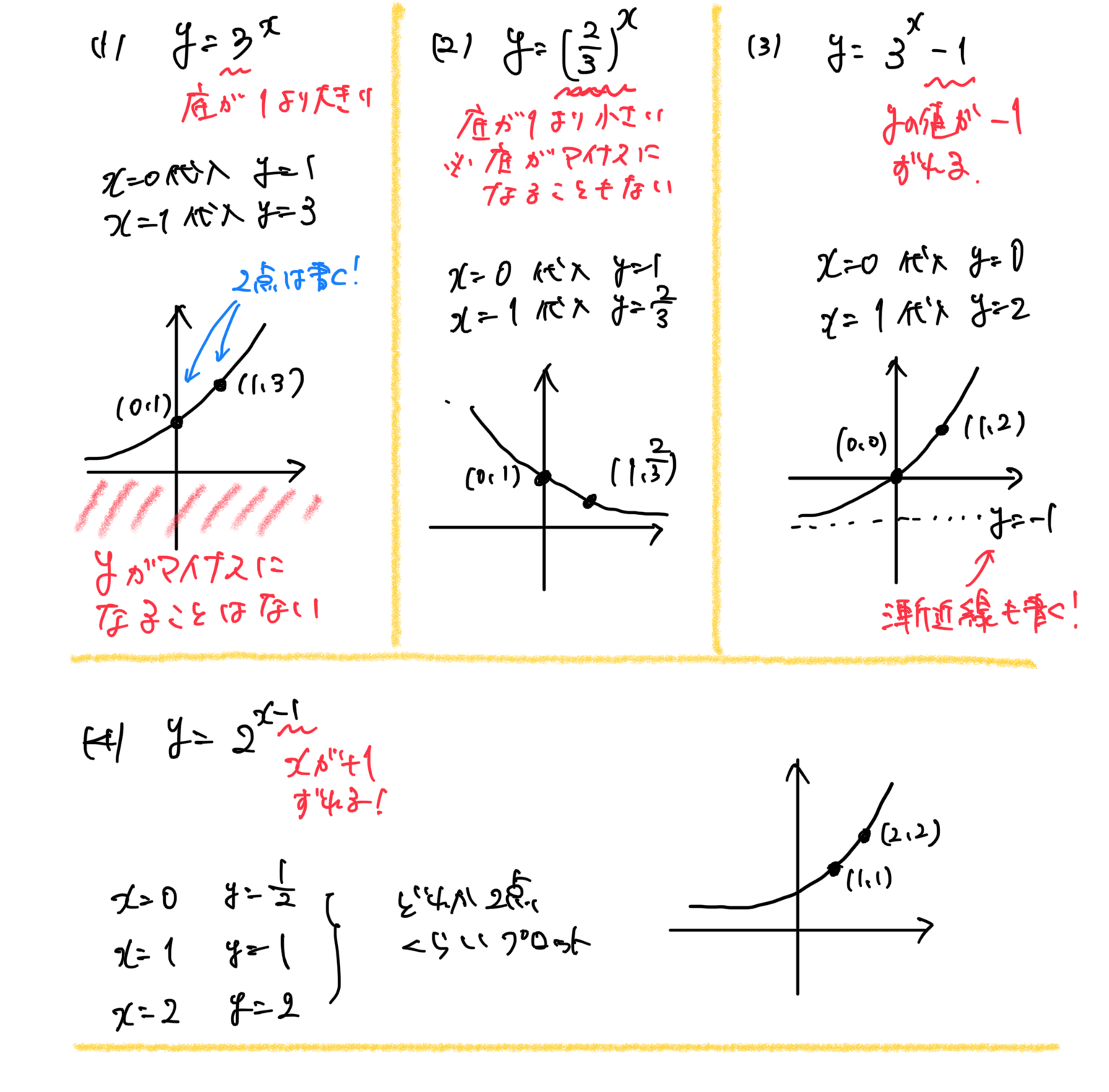
指数関数のグラフ
★グラフの形⇒xの値を変えて考えてみるとイメージがつく!
x乗の値は、マイナス乗から0乗、分数乗もあらゆる数値が考えられる。
xが何乗であったとしても、答えのyがマイナスになることはない。
底が1より大きいとき、xの値を大きくするとyも大きくなる
底が1より小さいとき、xの値を大きくするとyは小さくなる
底がマイナスはジグザグする(*底がマイナスは基本的には考えなくてよい)
xが0乗のとき、yの値は必ず1になる
xが1乗のとき、yの値は底と同じになる
★グラフの書き方
2点プロットする必要
yの値がずれているときは漸近線(ぜんきんせん)も書く
指数関数の方程式
★等式の対応する部分は同じであることを利用
底が同じであれば、指数の部分を下におろしてよい。
★文字に置き換えるとき範囲を考える
指数関数の値であるyの範囲
⇒必ずプラス。(グラフイメージ)
yをずらさない限り、マイナス乗も、分数乗もマイナスになることはない。
指数関数の不等式
★1<底のとき
底が同じであれば、指数部分の大小がそのまま値の大小となる。
★0<底<1のとき
底が同じであれば、指数部分の大小を逆にしたものが値の大小となる。
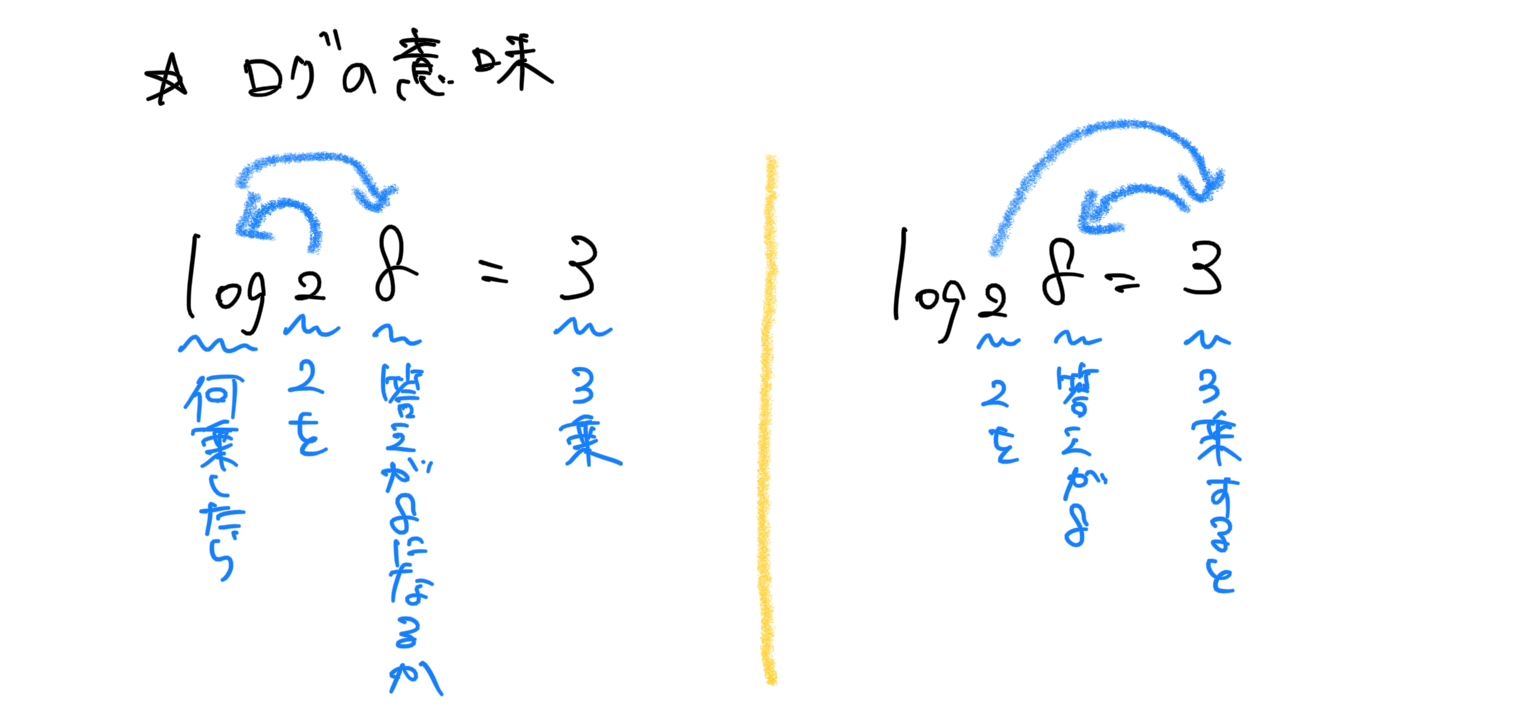
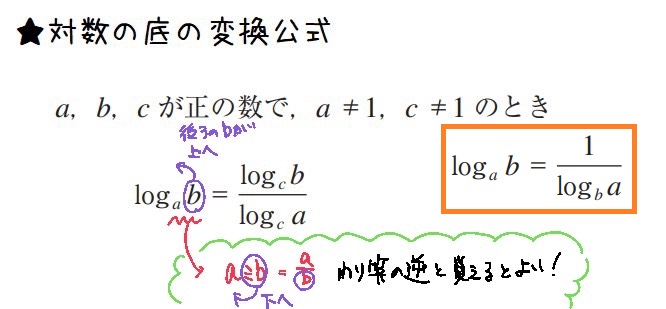
【対数】ログとは
★新しい記号 log
ルートと同じように考えると良い。
【対数】ログの計算
★ログの計算
底をそろえる!
★logの加減法
底がそろっていればできる。
(ルートと同じ。ログもある値なので、文字に変換してやると良い。)
足し算→真数どうしのかけ算になる
引き算→真数どうしの割り算
★logの乗除法
かけ算・わり算はできない。
約分で消すことはできる。
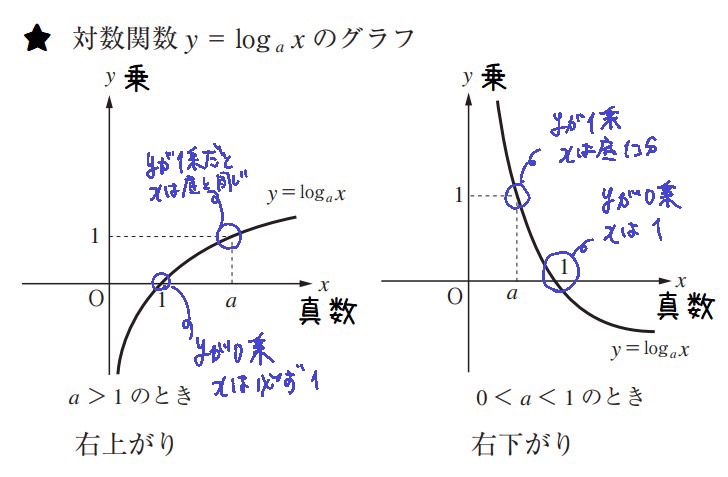
対数関数のグラフ
y=log底xの意味は、「底をy乗するとxになる」という意味
★グラフの形
xは真数なので、x乗の値がマイナスになることはない。
y乗の部分は、マイナス乗でもなんでもとりうる。
yが0乗なら、真数xは1
yが1乗なら、真数xは底と同じになる
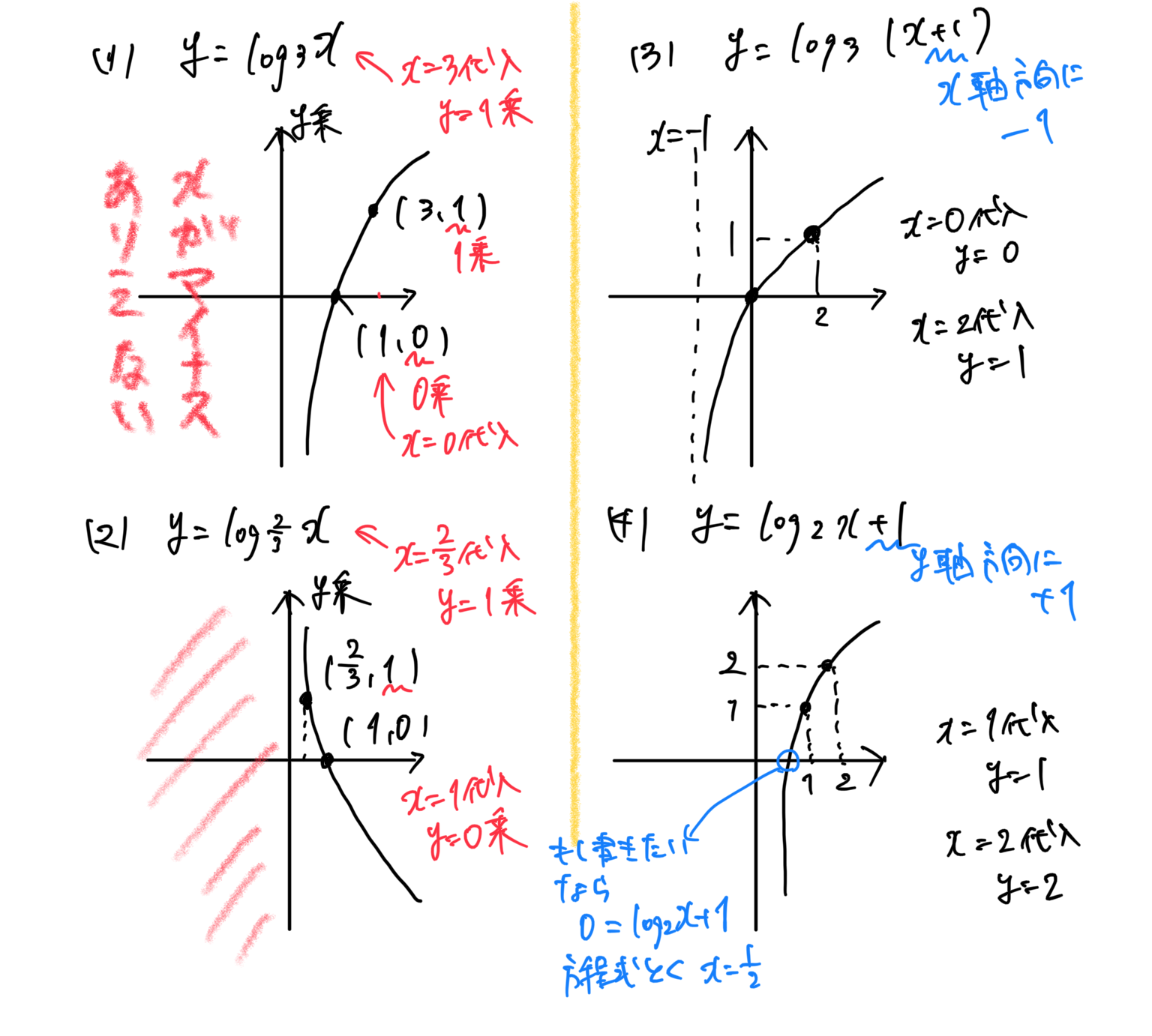
★グラフの書き方
2点プロットする必要
対数の方程式・不等式
【常用対数】10を底とする対数のこと
桁数を求める問題
小数第何位なのか(=小数第何位に初めて0でない数が現れるか)を求める問題
指数の問題は、対数logをとる(両辺にログをつけたす)ことで、下におろして計算ができるようになる
対数の大小と、真数の大小関係により、両辺にログをつけたして良い。
応用問題
この応用問題が終わったら、教科書傍用問題集(4step問題集など)が解けます。
4step問題集でドリル感覚で知識を整理して、青チャートで網羅的な知識を押さえると完璧です。
あとは、模試や入試の過去問などに取組みましょう。
暇があるときに、youtube動画で日本トップレベルの知識を身につけましょう。使えるものは、自分のためにとことん使ってください。
暇のある時に見たいyoutube解説動画
テストで9割以上が取れるコツ
1、教科書に記載されている基本問題や公式の、根本的な理解からマスターする。
2、青チャートか、フォーカスゴールドをマスターする。
*志望校によっては青チャートをやる必要はなく、教科書傍用問題集だけで足りる。
3、共通テスト過去問を解く
4、志望校の過去問を解く
受験ガチ勢チートでは、受験のプロが完全無料で、入試問題を丁寧にわかりやすく解説しています。
是非、チャンネル登録をお願いいたします↓↓
-120x120.jpg)
.jpg)


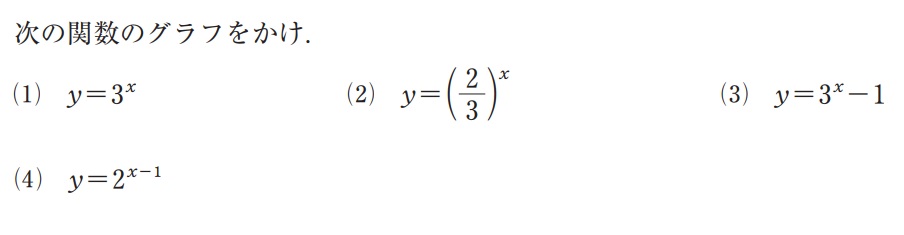
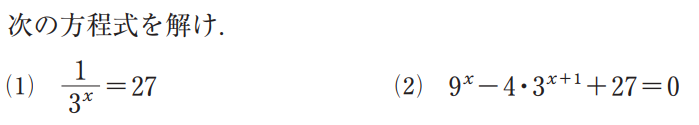



.jpg)
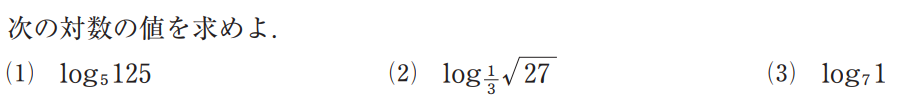

.jpg)
の解き方.png)