0から始める大学入試数学シリーズです。プロ教師がお届けします。
教科書レベル《必ずマスターすべき典型問題》
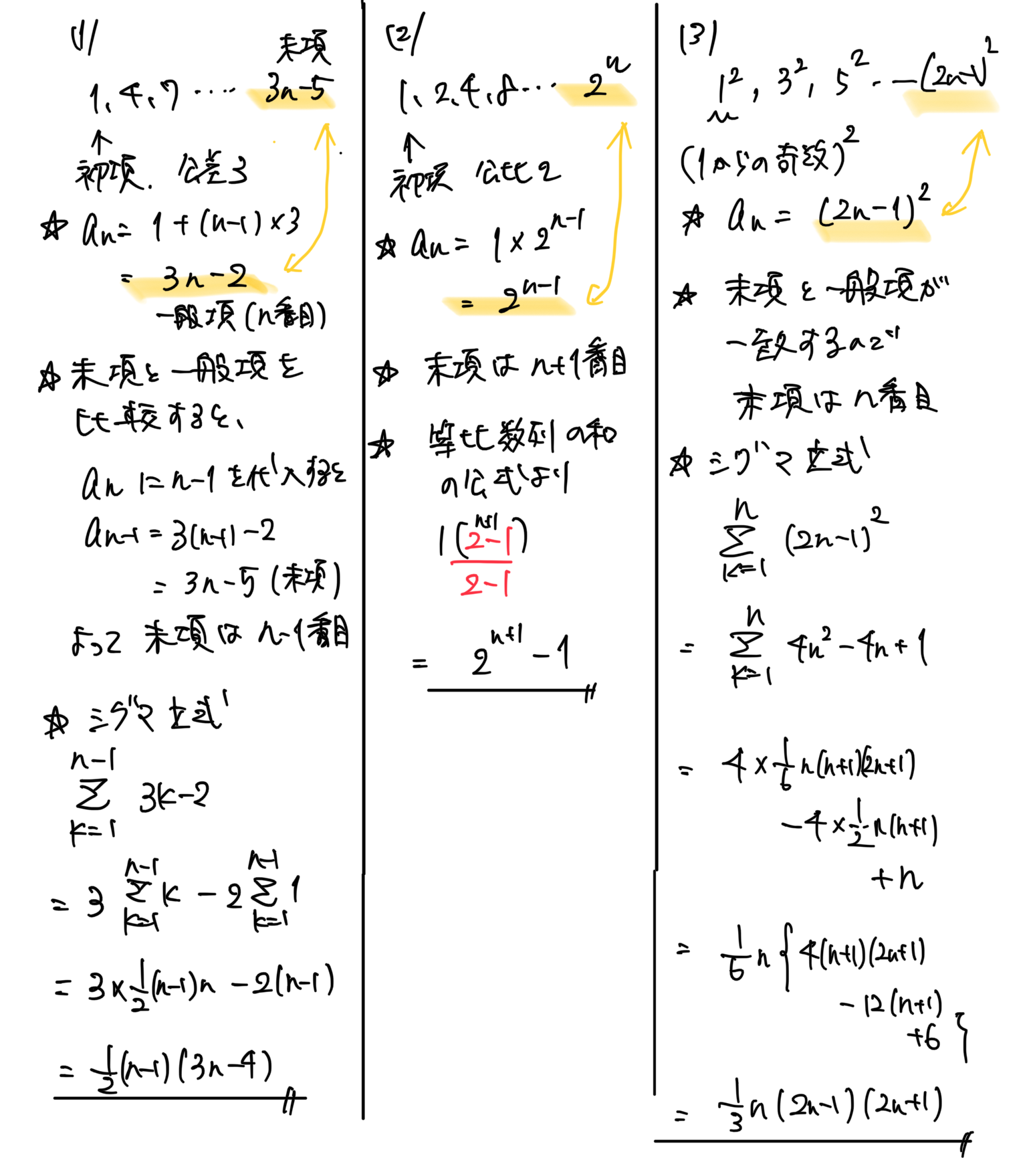
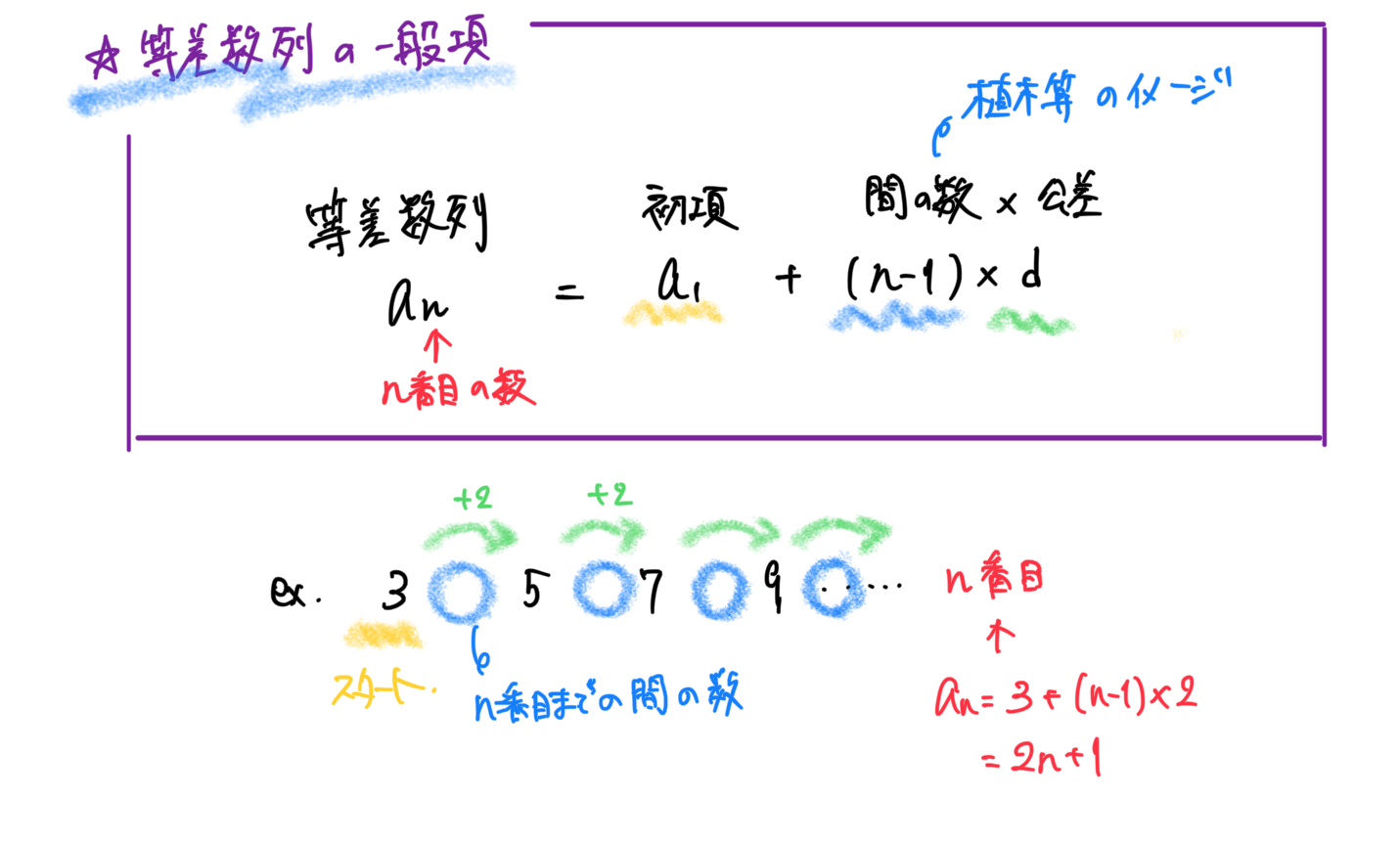
等差数列の一般項をもとめる問題
《考え方と解き方》
問題文に「等差数列」とあるので、数列が2つだけ分かれば十分。
あとは、公式にあてはめればOK
an = 1 + 5(n-1)
an = 5n -4
等差数列の一般項をもとめる問題②
《考え方と解き方》
等差数列の公式にあてはめて、初項をa 、公差をd として連立方程式を立てればOK
12 = a + 2d
-4 = a + 10d
これを解くと、d=-2 a=16
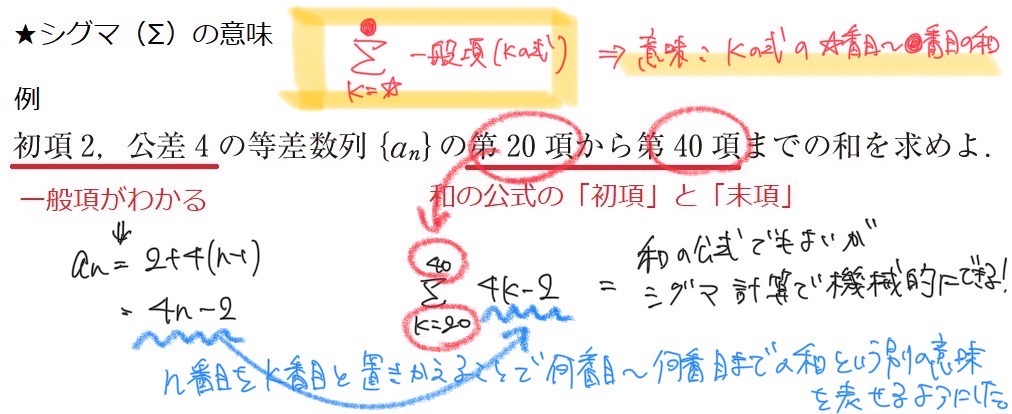
等差数列の和を求める問題
《考え方と解き方》
最適解:まず一般項を求めて、和の公式に代入。
この等差数列の一般項は、an = 2 + (n-1)×4 = 4n -2
等差数列の和の初項は、a=20を代入して、78
等差数列の和の末項は、a=40を代入して、158
項数は、40-20+1=21 *+1を忘れずに
あとは公式にあてはめて、(78+158)÷2×21=2478
別解:最初から和の公式Sをつくり、S40-S19をすれば良い。
等比数列の一般項を求める問題
《考え方と解き方》
問題文に「等比数列」と書いてあるので、数列の2つが分かれば公式に当てはめるだけ。
初項2 公比-3/2
$ an = 2・(- \frac{3}{2})^{n-1} $
*公比に分数やマイナスがあるとき、かっこを忘れずに。
等比数列の一般項を求める問題②
《考え方と解き方》<一般項を求める公式>に代入して連立方程式(代入法)を解けば良い。
$ 28 = ar^2 $
$ 224 = ar^5 $
上の式を、下の式へ代入すると $ r^3=8 $
移行して因数分解すると
$ r^3 – 8 = 0 $
$ (r-2)(r+2r+4)=0 $
解の公式を使うと、 $ r=2 , -1± \sqrt{3} i $
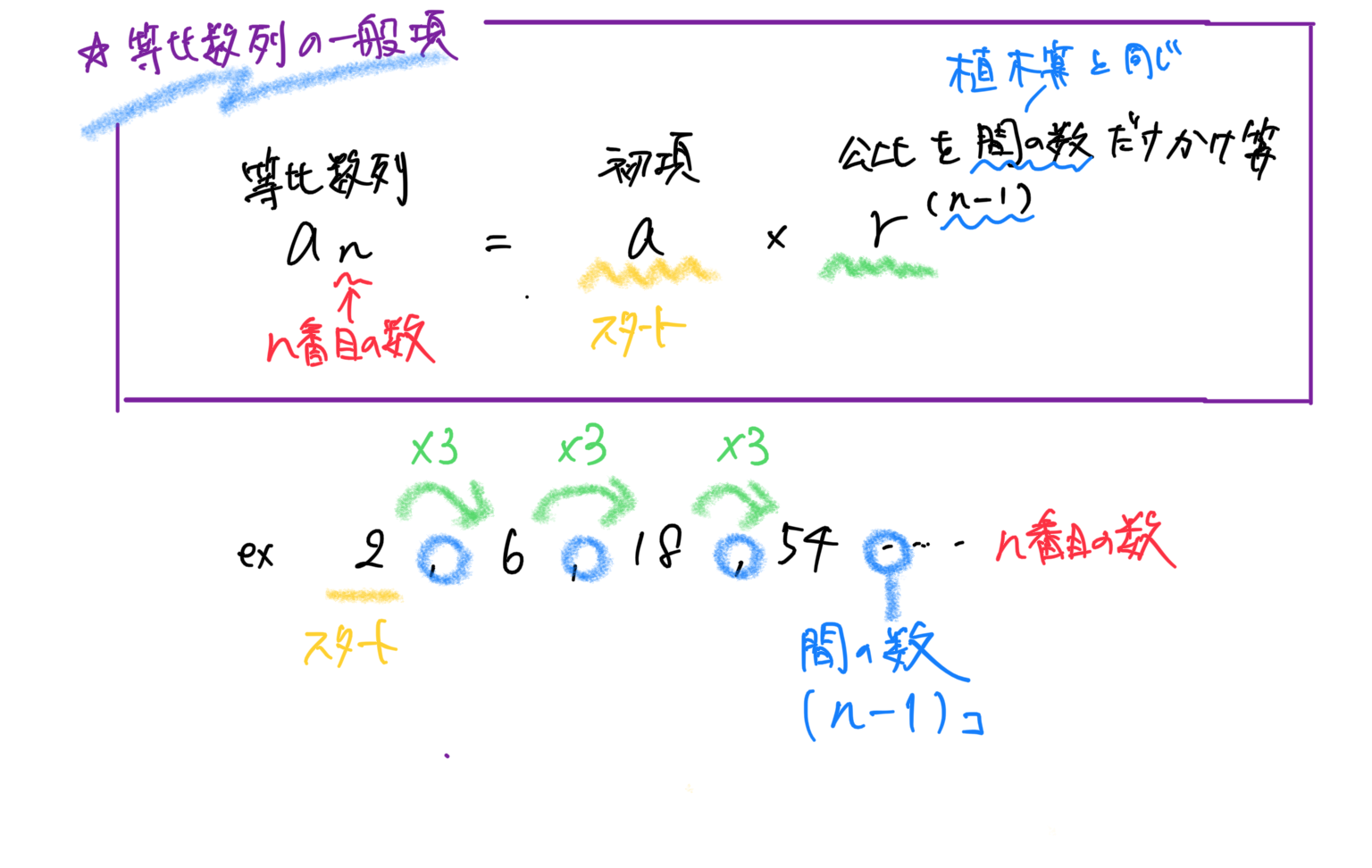
等比数列の和を求める問題
《考え方と解き方》
等比数列の和を求める問題②
《考え方と解き方》解法1:数列の初項と公式の初項を区別して考える解き方
別解:数列の初項と和の公式の初項を同じにして、S6-S2をして求める。
和の記号Σ(シグマ)とは
《考え方と解き方》
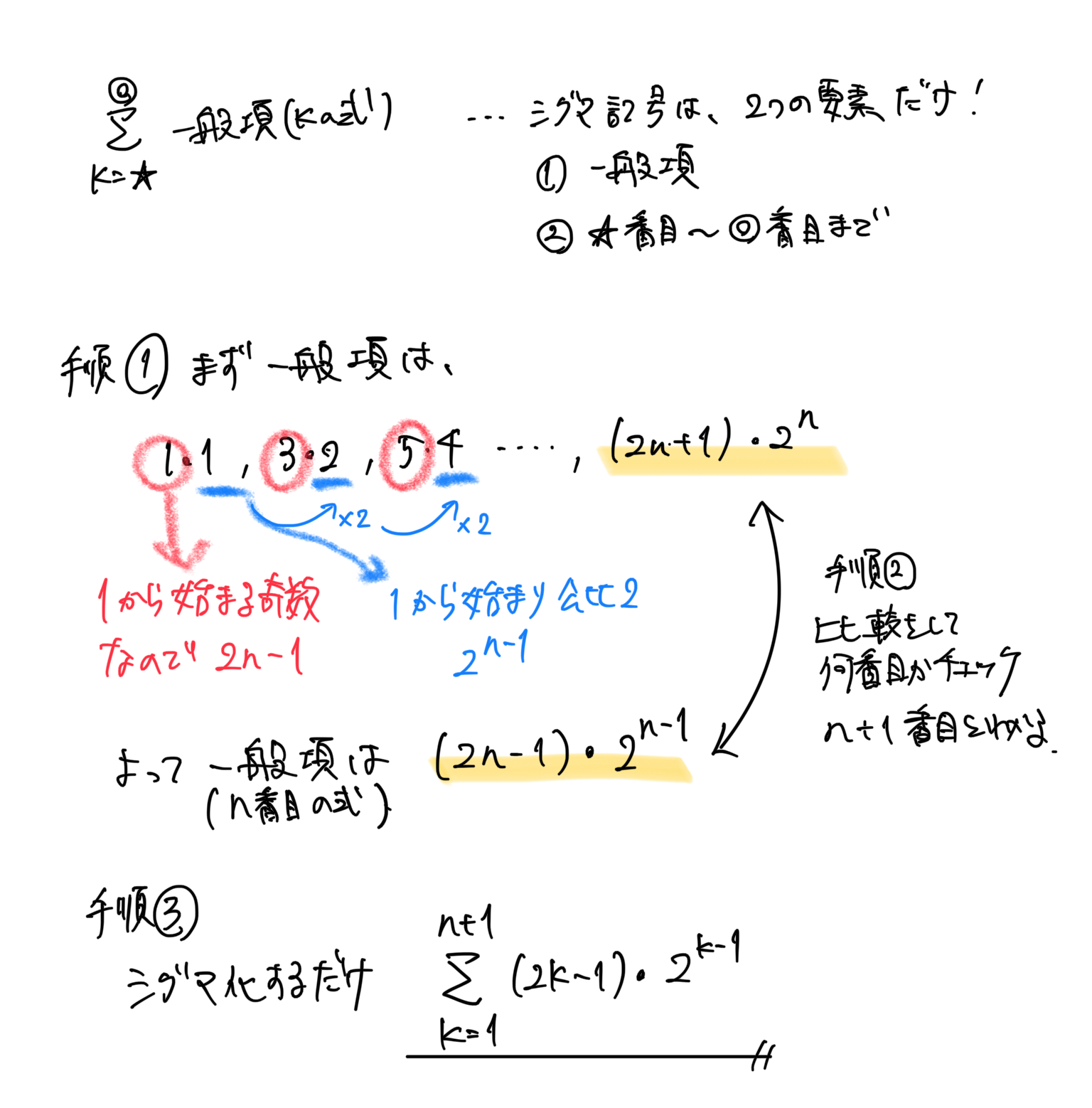
シグマ公式をあてはめる計算問題
等差数列や等比数列であれば和の公式があるが、それ以外の数列はシグマ計算をすることになる。
*等比数列は、シグマ計算公式がないので、初項や公比を求めて等比数列の和の公式を使うしかない。
《考え方と解き方》
シグマ公式をあてはめる計算問題②
《考え方と解き方》
階差数列(anの間の数に数列bnがある場合、bnをanの階差数列という)
【公式】階差数列を持つanの求め方:anの間の数にbnという数列がある場合、anはa1にbnの数列の和を足し算したものになる。
《考え方と解き方》
数列の和から一般項を求める問題
ポイント:anのそもそも意味が「n番目(末項)」の数を表していることを利用して、Snを書き並べて「Sn = a1 + a2 + a3 + … + an-1 + an 」、「a1 + a2 + a3 + … + an-1」の部分を引き算することで、末項(n番目)の数を求めることができる。
《考え方と解き方》
漸化式(ぜんかしき)とは
漸化式とは、いくつかの項から次に来る項を定義する式のこと。
式の意味を考えて、初項や公差などを出して、一般項を求めていく。
例 an+1 = an + 4 → 次の項(n+1番目の数) = 前の項(n番目の数)に+4したもの。つまり、等差数列。
《考え方と解き方》
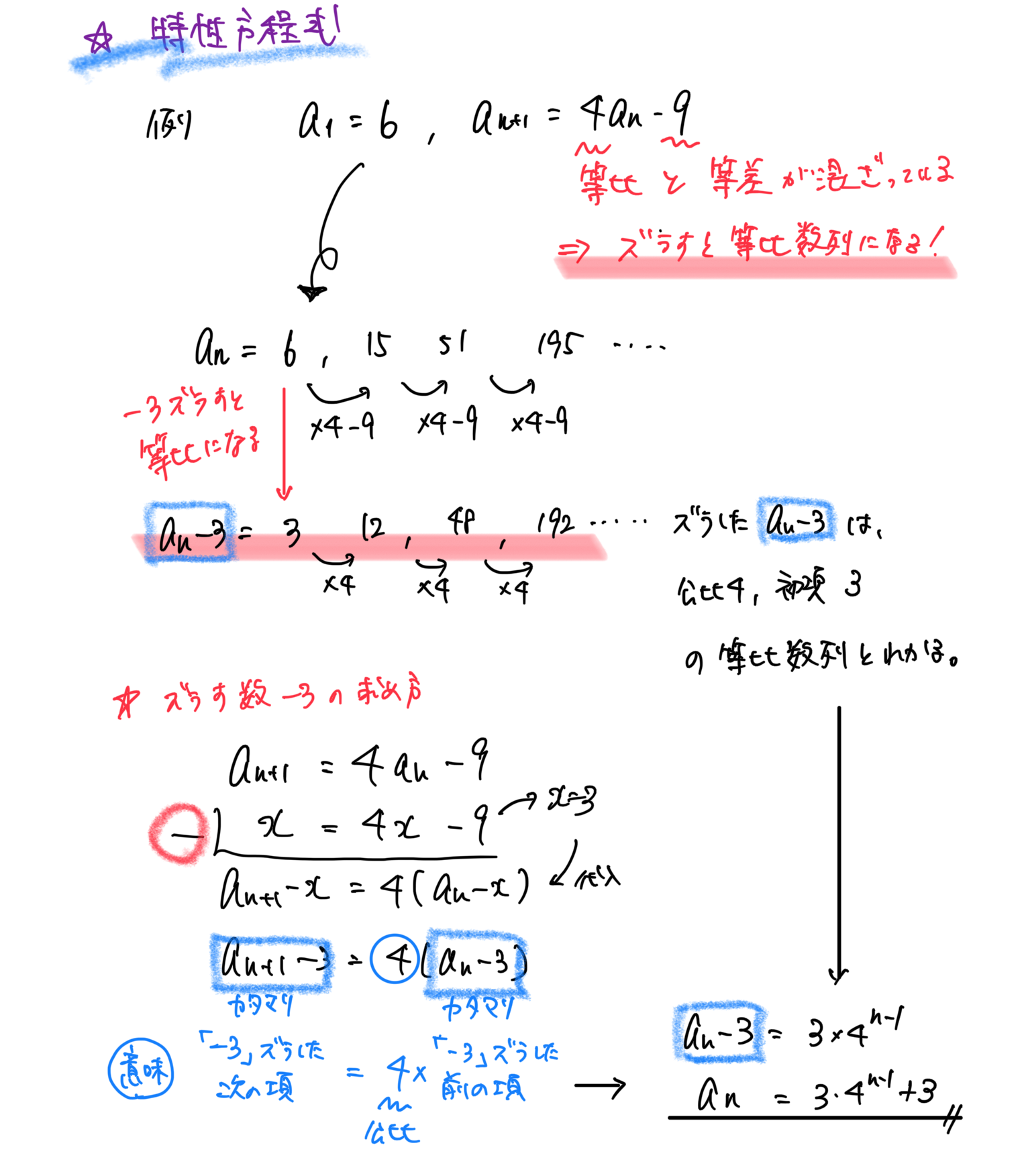
漸化式(特性方程式)
等差数列と等比数列が混ざったような形をした場合、式を変形して、等比数列として解いていく。
式の変形の仕方は、an+1とanを同じαと置いて、元の式と引き算をすることで変形できる。
変形が完了したら、検算として元の式と同じかどうか展開をして確かめると良い。
《考え方と解き方》
パート2
《考え方と解き方》
数学的帰納法(自然数で使える証明法)
等式の証明
手順:記述パターン暗記してあてはまめる
① n=1で、証明したい等式★が成立することを示す
② n=kで等式★が成立すると仮定
n=k+1にしたときも、等式★が左辺=右辺となり、成立することを示す。②の仮定を使ってよい。
③ ①②より、すべての自然数で成立
*数学的帰納法は自然数で使える証明方法なので、数列(n番目:断り書きをしない限り自然数の番号順となる)と相性が良い。
《考え方と解き方》
不等式の証明
等式と同じで、記述パターンにあてはまめる。
仮定の使い方で、不等式の代入は、等式の代入とは少し意味が違う点に注意。
例
| 等式の代入 | 不等式の代入 |
|---|---|
| A=B(仮定:Aを見たらBに変換して良い) A+C =B+C |
A<B(仮定:Aを見たらBに書き換えてよい) A+C <B+C |
《考え方と解き方》
推測される漸化式を数学的帰納法で証明
見たことのない漸化式は、いくつか書き出してみて法則(数列)を見つける。
その法則(数列)を証明するために、自然数の証明で役立つ数学的帰納法を使う。
数学的帰納法のn=k+1のとき、漸化式のK+1番目に、仮定を代入して証明していく。
《考え方と解き方》
群数列
ポイント
①最初から数えて「何番目(項数)」かを常にチェック
②何番目かという問題と、その値(一般項)は違うのでちゃんと区別すること。*文字式だと、何が何を表しているのか混同しやすい。
③末項が何番目かは、書き出して和の計算で求めやすい
⑤「何群の何番目か」という問題は、「全体の項数-手前の群の末項までの項数」で求められる。
《考え方と解き方》
応用問題
この応用問題が終わったら、教科書傍用問題集(4step問題集など)が解けます。
4step問題集でドリル感覚で知識を整理して、青チャートで網羅的な知識を押さえると完璧です。
あとは、模試や入試の過去問などに取組みましょう。
暇があるときに、youtube動画で日本トップレベルの知識を身につけましょう。使えるものは、自分のためにとことん使ってください。
暇のある時に見たいyoutube解説動画
テストで9割以上が取れるコツ
1、教科書に記載されている基本問題や公式の、根本的な理解からマスターする。
2、青チャートか、フォーカスゴールドをマスターする。
*志望校によっては青チャートをやる必要はなく、教科書傍用問題集だけで足りる。
3、共通テスト過去問を解く
4、志望校の過去問を解く
受験ガチ勢チートでは、受験のプロが完全無料で、入試問題を丁寧にわかりやすく解説しています。
是非、チャンネル登録をお願いいたします↓↓
-120x120.jpg)
.jpg)
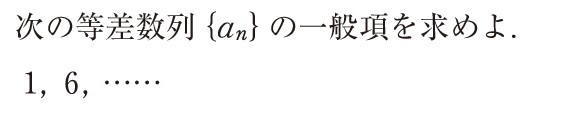



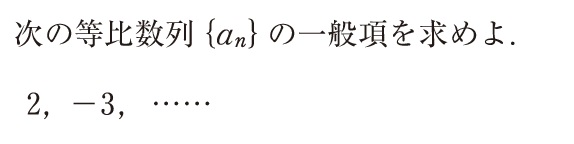





とは.jpg)
の公式適用問題.jpg)


の公式適用問題②.jpg)