【大学入試】化学～目次一覧～
第1編 物質の状態
粒子の結合と結晶の構造
物質の状態変化
気体
溶液
第2編 物質の変化
化学反応とエネルギー
電池と電気分解
化学反応の速さ・化学平衡 ⇒現在はここのページ
第3編 無機物質
非金属元素
金属元素Ⅰ 典型元素
金属元素Ⅱ 遷移元素
第4編 有機化合物
有機化合物の分類と分析
脂肪族炭化水素
アルコールと関連化合物
芳香族化合物
第5編 高分子化合物
天然高分子化合物
合成高分子化合物
計17章ほど
化学《化学反応の速さ・化学平衡》重要語句と典型問題まとめ・総チェック
反応の進み方
★反応の進み方
反応物が生成物に変化するまでに，遷移状態（または活性化状態）を経由している。
例 水素と酸素が化合して水が生まれる反応について、水素分子と酸素分子がそれぞれ２つの原子にバラバラに離れてから水分子として化合するのではなく、完全にバラバラに原子になったわけではなく中途半端な結合状態（これを活性錯合体、この状態を遷移状態、または活性化状態と呼ぶ）になった後、水分子として結合する。
★活性化エネルギーとは
反応物が遷移状態（活性化状態）になるために必要なエネルギーをさす。
＊活性化エネルギーは、吸熱反応（反応するにはエネルギーが必要）であり、反応後の物質のエンタルピーが上昇するという点で、結合エネルギーと似ている。
【化学】エンタルピー図の書き方（結合エネルギー、昇華エネルギー）
活性化エネルギーと触媒
★そもそも触媒とは
反応前後で触媒自身は変化せず，活性化エネルギーを低くする（反応速度を大きくする）物質のこと。
★触媒の種類
①均一系触媒：反応物と均一に混じり合う触媒
②不均一系触媒：反応物と均一に混じり合わない触媒
活性化エネルギーと温度
温度を上げると，活性化エネルギー以上のエネルギーをもった分子の割合が増える。
これにより，温度が高いほど，反応速度が大きくなる。
活性化エネルギーと濃度
濃度が大きくなると衝突回数が増加し，反応速度が大きくなる。
反応速度式（速度式）とは
★反応速度式（速度式）とは
反応速度ｙと反応物のモル濃度ｘの関係を表した式
だいたいの問題で、反応速度ｙは、反応物のモル濃度ｘの１乗の比例する式（一次関数）になることが多い。
例 ｙ＝速度定数a × ｘの１乗
★ここで速度定数とは
活性化エネルギーと温度で決まる定数のこと。
活性化エネルギーが小さいほど，また，温度が高いほど k が大きくなる。
★速度式は、実験によってしかわからない。
一応、目安となる式として、化学反応式の係数を使って表せるものがある。
化学反応 AとBからCが生成される式だとすると（m A + n B → i C ），
反応速度ｖは、比例定数ｋ×[Aの濃度]Aの係数乗・[Bのモル濃度]Bの係数乗 になる。
反応速度式 $ v = k[A]^m [B]^n $
例題
２A + B → ２C という反応がある。
AとBの２つのものから、Cが生成している。
Aのモル濃度をX、Bのモル濃度をX’、反応速度ｙとする。
A のモル濃度のみを 2 倍にしたところ，C の増加速度も 2 倍になり，B のモル濃度のみを 2 倍にしたところ，C の増加速度は４倍になった。
このことから、ｙとｘの関係式を答えなさい。ただし、速度定数はｋとする。
解答
ｘが２倍になるとｙも２倍→１乗の比例関係
ｘ’が２倍になると、ｙは４倍→２乗の比例関係
よって、ｙ＝ｋ・ｘ^1 ・ｘ’^2
反応速度式を求める実験
★計算方法
濃度の平均は、２つの区間の濃度の足し算÷２区間
反応（濃度変化）の速度の平均は、２つの区間の濃度の引き算÷時間
比例定数ｋの求め方は、反応速度の平均ｙ÷度の平均ｘ
【高校化学】反応速度式を求める実験
化学平衡の状態(平衡状態)とは
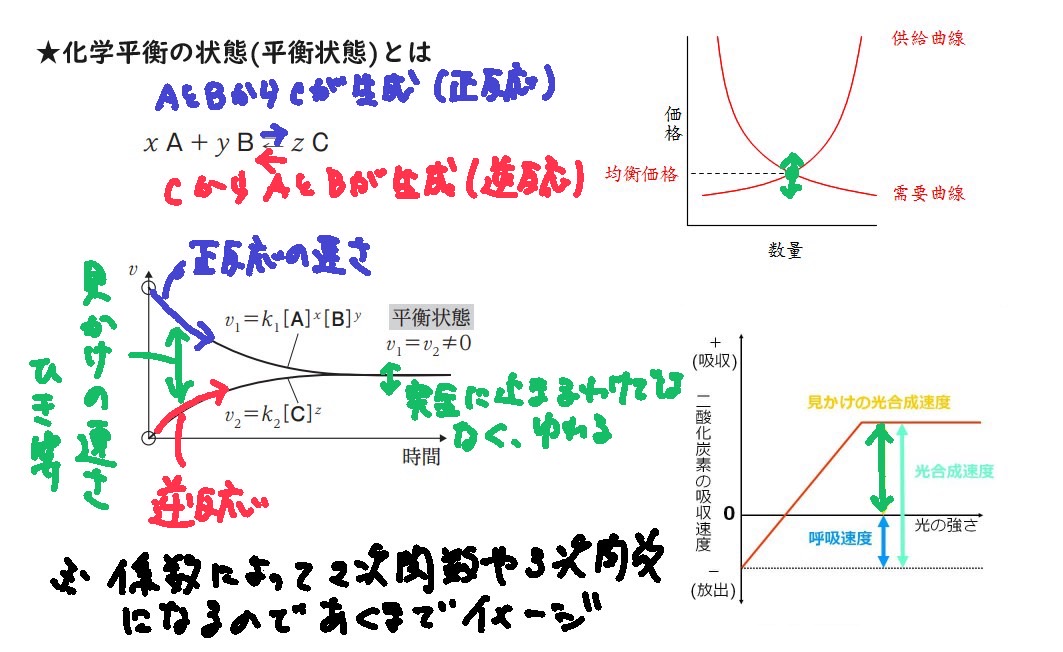
★化学平衡の状態(平衡状態)とは
可逆反応において，正反応と逆反応の速さが一致し，見かけ上反応が停止した状態。
＊社会のキーワードで言うと需要と供給が一致する「市場価格」のイメージ
化学平衡の図
・正反応の速さは、maxからスタートし、傾きが下降していく（係数によっては2次関数や3次関数になる）
・逆反応は、生成物cができた瞬間に逆向きの反応が起こり始めるので、原点からスタート。
・y座標の差が「見かけの反応速度」を表す。生物でいうと「呼吸と光合成の二酸化炭素の見かけの光合成速度」と似ている
・平衡と言っても、止まったように見えるものとするだけで、実際はてんびんのようにどちらかに振れているので、完全にv1ーv2＝0ではない。
【高校化学】化学平衡の状態(平衡状態)とは
化学平衡（質量作用）の法則とは
化学平衡（質量作用）の法則
可逆反応が平衡状態にあるとき、反応速度が同じであるから、以下の式が成立する。
正反応の速さをV1、逆反応の速さをV2とすると
$ v1 = k1[A]^x[B]^y $
$ v2 = k2[C]^z $
平衡状態だとv1≒v2であるから、右辺どうしも同じになる。（正確にはイコールではない）
$ k1[A]^x[B]^y = k2[C]^z $
これを変形させて
$ \frac{k1}{k2} = \frac{[C]^z}{[A]^x[B]^y} $
＊ $ \frac{k1}{k2} $ は定数となり、これを平衡定数という（Kcで表現されることが多い）。
＊「 左辺のモル濃度の積 分の 右辺のモル濃度の積 」と覚えよう。
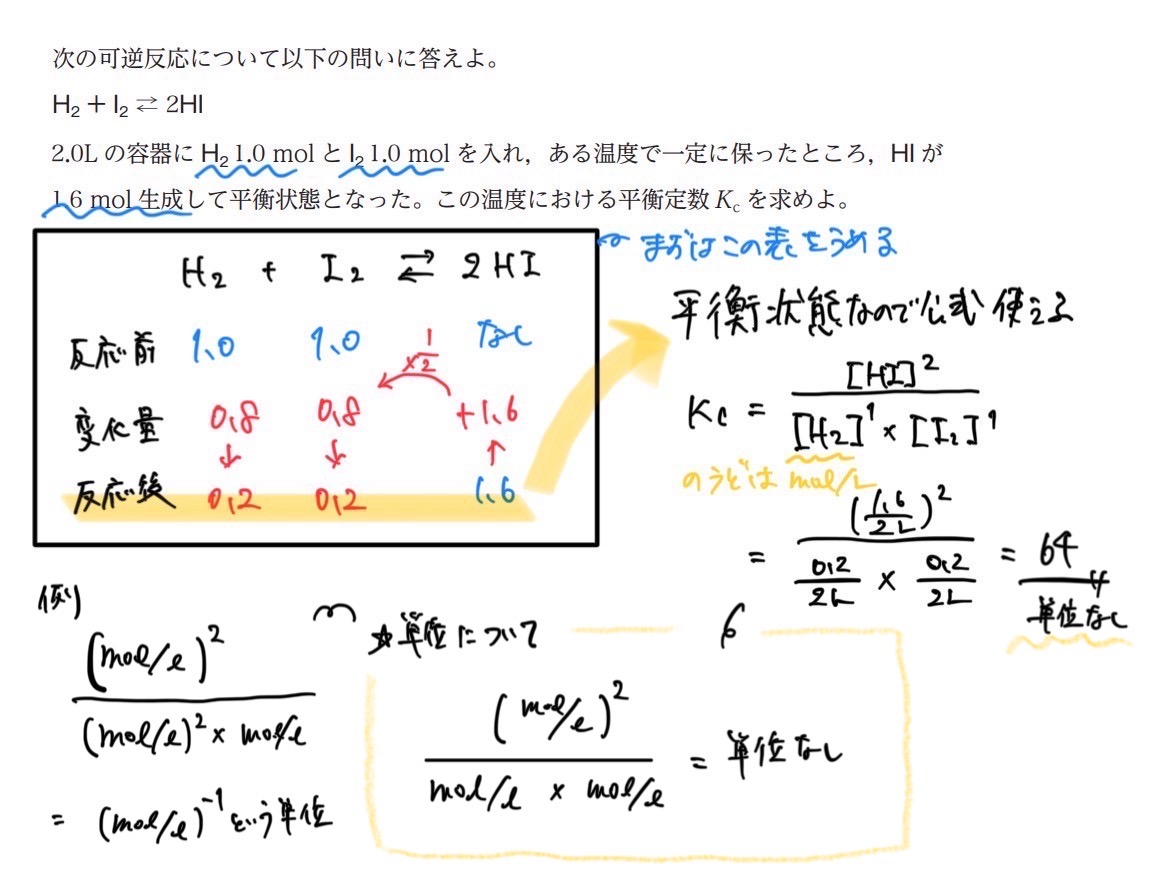
化学平衡の法則の計算のコツ
①反応式を書く
②反応前、変化量、反応後のモルの変化を書く
③反応後（平衡状態）のモルを使って、化学平衡（質量作用）の法則の公式にあてはめて計算
＊公式はモル濃度(mol/L)なので、図のモルに体積で割ることを忘れずに。
④単位（分母と分子のモル濃度）に注意
【高校化学】化学平衡の法則の計算のコツ
化学平衡の法則を気体で考えてみる
AとBからＣができる、という化学反応 xA + yB ⇔ zC のA・B・Cの部分が、もし気体であったなら、気体の状態方程式を代入することができる。
化学平衡の法則のモル濃度 $ [A]^x [B]^y [C]^z $ (mol/L)の部分に、
$ Kc = \frac{[C]^z}{[A]^x[B]^y} $
気体の状態方程式 PV=nRT をモル濃度 $ \frac{n}{v} $ (mol/L)で変形した式を
$ \frac{n}{v} = \frac{p}{RT} $
代入すると、
$ Kc = \frac{ [\frac{pc}{RT}]^z }{ [\frac{pa}{RT}]^x \times [\frac{pb}{RT}]^y } = \frac{ (pc)^z }{ (pa)^x \times (pb)^y } \times (RT)^{x+y-z} $
そもそもKcが定数なので、等式で左辺が定数なら右辺も定数になるので、
$ \frac{ (pc)^z }{ (pa)^x \times (pb)^y } $ の部分を圧平衡定数をいい、Kpで表現される。《左辺の分圧の積 分の 右辺の分圧の積》で覚えよう！
$ Kp = \frac{ (pc)^z }{ (pa)^x \times (pb)^y } $
結局、平衡定数Kcは、圧平衡定数Kp使って、以下の式で表現される。
$ Kc = Kp \times (RT)^{x+y-z} $
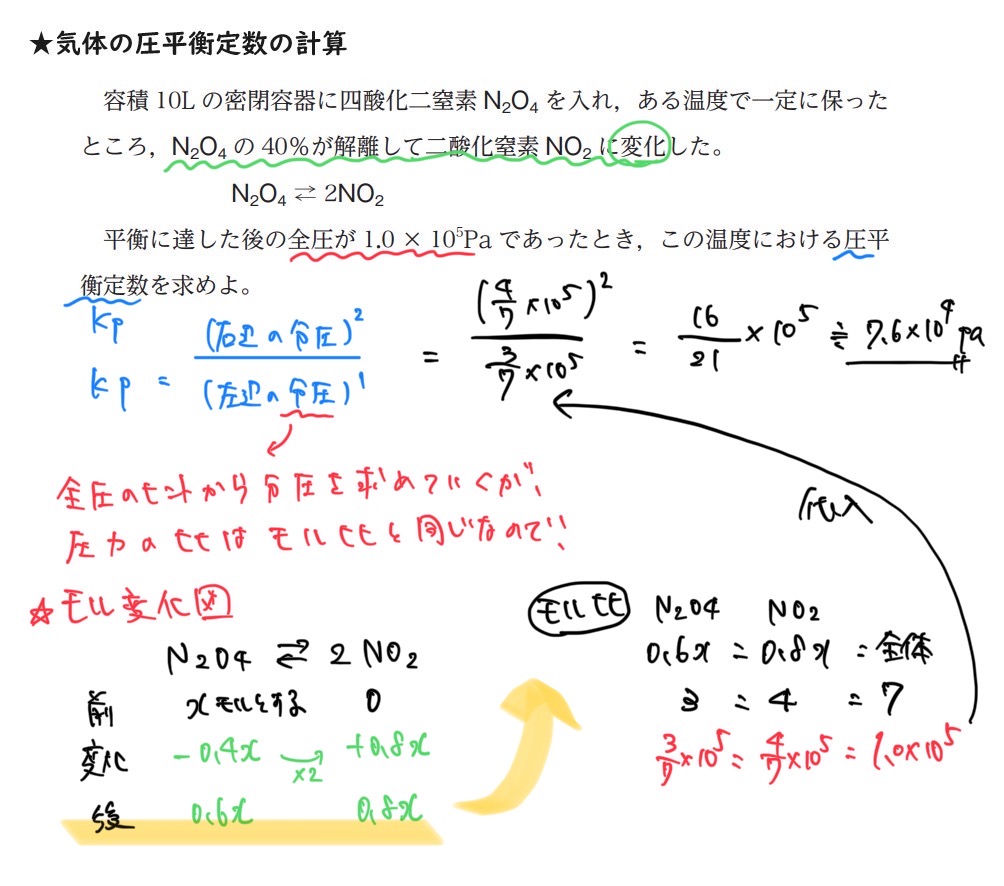
①圧平衡定数を求めるには分圧pa,pb,pc,pd…が必要
②分圧を求めるために、モル比を求める
③モル比から問題文のヒントを使って分圧がわかるので、公式に代入
《公式》圧平衡定数Kp
$ Kp = \frac{ (pc)^z }{ (pa)^x \times (pb)^y } $
＊『左辺の分圧の積 分の 右辺の分圧の積』で覚えよう！
【高校化学】圧平衡定数の計算問題のコツ
平衡状態の移動とその条件（ルシャトリエの原理）
★ルシャトリエの原理とは
化学反応が平衡状態にある場合において，平衡状態を決定する３つの原因（①温度②濃度③圧力）を変化させると，その影響を緩和する方向へ平衡移動する。
ここで「影響緩和方向」とは、３つそれぞれの方向を考える必要がある。
＊温度・濃度・圧力以外の条件では平衡移動は起こらない。
温度の場合の場合の「影響緩和方向」とは
個別具体的に、エンタルピー変化から矢印の向きが何の反応を示しているかをチェックしなければならない。
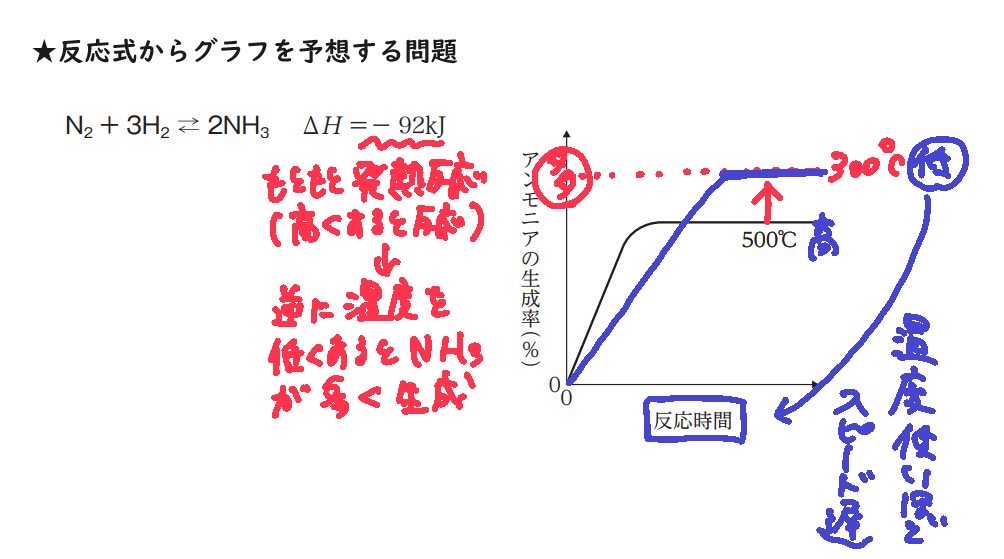
例１ N2 + 3H2 ⇄ 2NH3 ΔH ＝− 92kJ において、温度を上げるとどうなるか？
エンタルピー変化がマイナスなので、右⇒の反応が発熱反応だとわかる
化学反応が平衡状態にあるとき，温度を上げると右⇒の反応が進んでしまうので、
平衡状態を保つために左⇐の吸熱反応が進む（影響緩和方向）
よって、例１の場合で、かつ温度を上げたときの「影響緩和方向」とは、左⇐の吸熱方向へ平衡移動が進む方向をさす。
例２ N2O4 ⇄ 2NO2 ΔH ＝ 57kJ において、温度を下げるとどうなるか？
エンタルピー変化がプラスなので、右⇒の反応が吸熱反応だとわかる
温度を下げると右⇒の反応が進むため、
「影響緩和方向」への力が強くなり、左⇐の発熱方向へ平衡移動が進む。
濃度の場合の「影響緩和方向」とは
温度の場合と同じように、「平衡（バランス）を保つために」を考えると良い。
＊固体を加えても濃度変化しない。
例 NH3 + H2O ⇄ NH4 + OH − の反応において、HClを中和点に達しない程度に加えた場合どうなるか？
HClを加えると、右辺のOH− が減少するので、
バランスを保つために
右⇒の反応が進む。
例 N2 + 3H2 ⇄ 2NH3 において、N2 だけを加えて濃度を高くするとどうなるか？
左辺のN2 の濃度が高くなるので、
バランスを保つために
N2 が減る反応、つまり右⇒の反応が進んで、アンモニアができる。
例 C（固）+ H2O（気） ⇄ H（気） 2 + CO（気） において、C（固）を少量加えるとどうなるか？
固体を加えても、固体の濃度は変化しない（イメージ：少なくなったコーラのグラスに、コーラを加えても同じ味・濃度）
濃度が変化しないので、反応の移動もしない。
圧力の場合の「影響緩和方向」とは
圧力は、粒の数（mol）でバランスを考えるとよい。
圧力を上げると、壁を叩く力が増えるから、
バランスをとるために、粒の数を減らせば壁を叩く力が弱くなる。
粒の数は、両辺の係数を見れば良い。
固体であれば気体の粒の数としてカウントしない。
例 N2 + 3H2 ⇄ 2NH3 において、圧力を上げたらどうなるか？
左辺の係数を見ると、物質量（粒の数）は４
左辺の係数を見ると、物質量（粒の数）は２
よって、バランスを保つために物質量（粒の数）を少なくなる方向に移動するから、右向きに反応が進む。
例 C（固）+ H2O（気） ⇄ H（気） 2 + CO（気） において、圧力を上げたらどうなるか？
左辺の係数を見ると、物質量（粒の数）は１ ＊固体はカウントしない
左辺の係数を見ると、物質量（粒の数）は２
よって、バランスを保つために物質量（粒の数）を少なくなる方向に移動するから、左向きに反応が進む。
例 N2 + 3H2 ⇄ 2NH3 において、体積一定で Ne を加えるとどうなるか？
体積が一定であれば、PV＝NRTより、圧力Pも変化していない。
よって、反応の移動もしない。
例 N2 + 3H2 ⇄ 2NH3 において、圧力一定で Ne を加えるとどうなるか？
圧力一定（大気圧で保たれる）であれば、１つ１つの分圧が変化する（Neを入れることでそれぞれ小さくなる）ので、
分圧が下がったことを意味するので、
左辺の係数を見ると、物質量（粒の数）は４
左辺の係数を見ると、物質量（粒の数）は２
よって、バランスを保つために物質量（粒の数）を多くなる方向に移動するから、左向きに反応が進む。
アンモニアの工業的製法とルシャトリエの原理
商品として、多くのアンモニアを作るために、ルシャトリエの原理が使われている。
アンモニアの反応式より、
N2 + 3H2 ⇄ 2NH3 ΔH ＝− 92kJ
温度について
発熱反応であるから、ルシャトリエの原理より、アンモニア（右辺）を作るために、
温度を下げる（400～600℃）と、右の反応が進んでアンモニアが生成できる。
圧力について
左辺の粒の数（物質量）は、係数を見ると４
右辺の粒の数（物質量）は、係数を見ると２
ルシャトリエの原理より、圧力を上げる（1 × 107 〜 3 × 107Pa）と粒数が少なくなる方向（右方向）に反応が進んでアンモニアが生成できる。
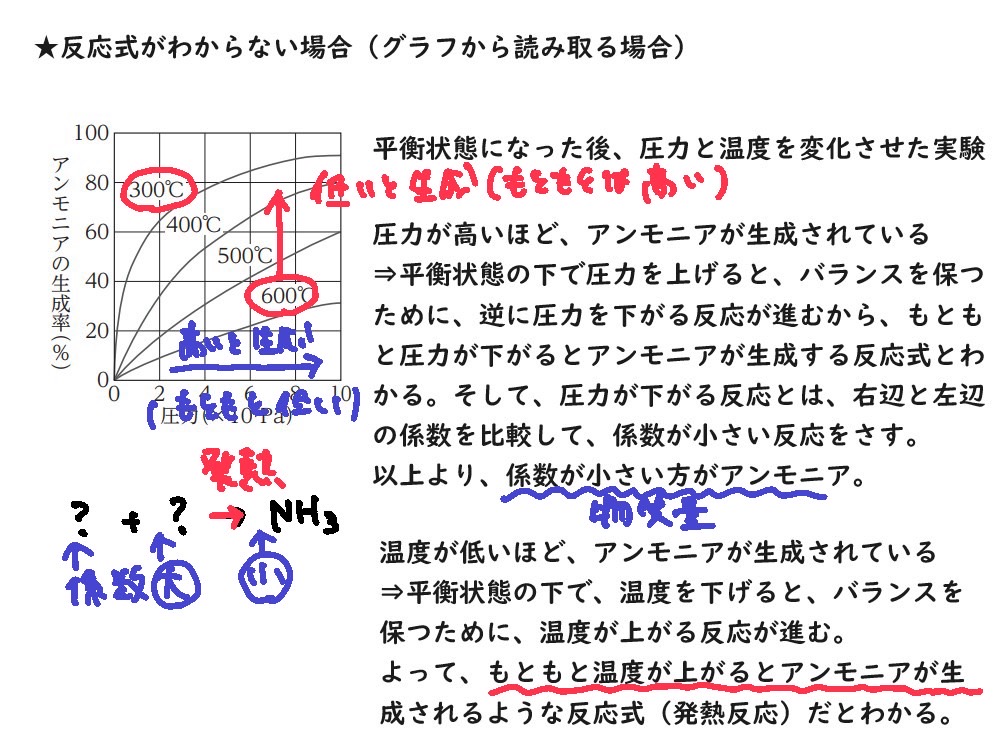
ルシャトリエの原理をグラフから考える問題
前提として平衡状態である、ということはチェック。
いずれの問題も、平衡状態から圧力や温度を変化させるとどうなるか？という問題。
平衡状態であれば、バランスを保つために逆の反応が進むことを考えていけばよい。
【高校化学】ルシャトリエの原理をグラフから考える問題②
【高校化学】ルシャトリエの原理をグラフから考える問題①
平衡状態は水でも起こっている
平衡状態（可逆反応）は、水でも起こっている。
H2O ⇄ H+ + OH − ΔH ＝ 56.5kJ
この反応式に、化学平衡の法則の公式をあてはめてみる。
化学平衡の法則のモル濃度 $ [A]^x [B]^y [C]^z $ (mol/L)の部分に、$ [ H_{ 2 } O] [OH^-] [H^+] $ をあてはめる。
$ Kc = \frac{[C]^z}{[A]^x[B]^y} $
$ Kc = \frac{ [OH^-] [H^+] }{ [ H_{ 2 } O] } $
分母を払うと、
$ Kc [ H_{ 2 } O] = [OH^-] [H^+] $
＊定数はKcではなく、Kwを使うことが多い。この $ Kw = [OH^-] [H^+] $ を水のイオン積という。
水のイオン積 $ Kw = [OH^-] [H^+] $ は平衡定数であるため，温度が変わらない限り一定である。
25℃のとき, 1.0 × 10−14(mol2/L2)となる。
温度を変えるとどうなるか？
水の反応式は、エンタルピー変化がプラスであることから、
正反応（右向き⇒の反応）が吸熱反応（温度が下がる反応）になる。
よって、ルシャトリエの原理より、逆に、温度を上げることで水の正反応（右向き⇒の反応）、つまり電離が進んで濃度が大きくなる。
つまり、２５度より温度を上げると、水のイオン積 Kw は、1.0 × 10−14(mol2/L2)より大きくなる。
弱酸・弱塩基も可逆反応（平衡状態）
例 酢酸 CH3COOH ⇄ CH3COO − + H+
一部しか電離しておらず，化合物とイオンが共存し平衡状態となっている。
このような電離による化学平衡を電離平衡とよび，平衡定数（電離定数）を用いて考えていく。
そもそも弱酸・弱塩基とは
電離度α が１未満の酸と塩基をさす。
ここで電離度α とは
溶解している酸・塩基のうち、電離している酸と塩基の割合を示す
式：電離度α＝（電離している酸 ・ 塩基）÷（溶解している酸・塩基）
ちなみに、
強酸・強塩基は、電離度が1（100%）であり、元に戻ることのない不可逆反応。
よって、平衡状態（行ったり来たり反応バランスを保ってる状態）になることもない。
強酸（H2SO4・HCl・HNO3）
強塩基（KOH・NaOH・Ba(OH)2・Ca(OH)2）
＊これら暗記すべき強酸・強塩基以外が弱酸・弱塩基と覚えよう！
強酸・強塩基のpH計算
pHは指数部分を表示したいがゆえに、常用対数（log10）が使われる。
※対数の底は10。省略されることが多い。
pH =− log10[H+]
[H+] = [ 酸 ] ×価数×電離度α
・強塩基のpH計算
pOH =− log[OH− ]
[OH− ] = [ 塩基 ] ×価数×α
・pH + pOH = 14
＊強酸・強塩基は、電離度が1（100%）であり、元に戻ることのない不可逆反応。
よって、平衡状態（行ったり来たり反応バランスを保ってる状態）になることもないため、平衡定数を考えることもない。
【高校化学】強酸・強塩基のpH計算
弱酸・弱塩基のpH計算
弱酸・弱塩基のpH計算は、中和反応を具体例として、３つの場面で使う公式が異なる。
① 滴定前（弱酸のみの電離平衡の計算となる）
例 酢酸のみ CH3COOH ⇄ CH3COO− + H+
② 滴定後、中和点前（緩衝液）
例 未反応の弱酸と，反応により生じた弱酸の塩の混合溶液《酢酸と酢酸ナトリウムの混合水溶液》
CH3COOH ⇄ CH3COO− + H+
CH3COONa → CH3COO− + Na+
③ 中和点（塩の加水分解）
例 塩の水溶液
CH3COONa → CH3COO − + Na+
CH3COO − + H2O ⇄ CH3COOH + OH −
【高校化学】弱酸・弱塩基のpH計算は、中和反応を具体例として、３つの場面で使う公式が異なる。
滴定前（弱酸・弱塩基のみの電離平衡の計算）
pH =− log10[H+]
[H+] = [ 酸 ] ×価数×電離度α
[H+] = $ \sqrt[]{初期濃度c \times 電離定数Ka } $
＊弱酸の初期濃度を c mol/L，電離定数を Ka とする。
＊電離度αが１に比べて非常に小さく、１−α≒１とみなしたときに使える公式
＊弱塩基の計算も、同様に考えることができる。
【高校化学】弱酸・弱塩基のpH計算
滴定後、中和点前（緩衝液）のpH計算
例 中和反応の初めの方
酢酸に水酸化ナトリウムを加える
→酢酸と酢酸ナトリウムの混合水溶液ができる。
この混合物において、
CH3COOH ⇄ CH3COO− + H+ …①
CH3COONa → CH3COO− + Na+ …②
★緩衝液とは
弱酸とその塩の混合水溶液，または弱塩基とその塩の混合水溶液。
例 酢酸と酢酸ナトリウムの混合水溶液
★緩衝液の緩衝作用とは
少量の酸や塩基を加えても，pH はほぼ一定に保たれる。このようなはたらきを、緩衝作用という。
中和滴定でさらに水酸化ナトリウムを加えても、①のH +がなくなって水ができるため、補充するかのごとく→の反応が進む
逆にここで、酸を加えたとしても、①の酢酸イオンが酢酸に変化するため、補充するように、→の反応が進む
pH =− log10[H+]
$ [H+] ＝ Ka \times \frac{弱酸の初期濃度mol/l}{塩の初期濃度mol/l} $
＊Kaは弱酸の電離定数
＊分数なので、塩と酸の比がわかれば良く、正確な濃度がわかる必要はない。
【高校化学】緩衝液（弱酸とその塩の混合水溶液）の pH計算
【高校化学】滴定後、中和点前（緩衝液）のpH計算
中和点（塩の加水分解）のpH計算
そもそも加水分解とは
水を加えることで、その水が反応物と反応し（化合物の結合を切る）、分解反応を起こすことをさす。
例 CH3COONa（弱塩基性）は、なぜ弱塩基性なのか？
CH3COONa → CH3COO − + Na+ …塩は水中で完全に電離する。
CH3COO − + H2O ⇄ CH3COOH + OH − …弱酸由来の酢酸イオンCH3COO − が加水分解（水（水素イオンH+） と出会って、酢酸CH3COOH に戻り、水酸化物イオンOH −が残る）を起こすため。
例 NH4Cl（弱酸性）は、なぜ弱酸性なのか？
NH4Cl → NH4+ + Cl − …塩は水中で完全に電離する。
NH4+ + H2O ⇄ NH3 + H3O+ …弱塩基由来のアンモニウムイオンNH4+ が加水分解（水（OH-） と出会って、アンモニアNH3 に戻り、オキソニウムイオンH3O+（H2OとH+ ）が残る）を起こすため。
pH = 14 – pOH
pOH =− log[OH− ]
$ [OH− ] = \sqrt[]{ \frac{塩の濃度 \times 水のイオン積}{弱酸の電離定数} } $
平衡状態は沈殿物でも起こっている
例 塩化銀
AgCl（固） ⇄ Ag+ + Cl －
難溶性の塩（いわゆる沈殿）は、水中でわずかに溶解して溶解平衡の状態になっている。
AgCl の溶解平衡において，
平衡定数Kは、「 左辺のモル濃度の積 分の 右辺のモル濃度の積 」より、
$ K = \frac{[Ag^+][Cl^－]}{[AgCl（固）]} $
固体は結晶であり濃度は一定なので，[AgCl（固）] を,平衡定数 K とまとめて一つの定数とできる。
K[AgCl（固）] ＝ Ksp ＝ [Ag+][Cl－]
K[AgCl（固）] の定数を,溶解度積 Ksp という。
溶解度積は、平衡定数であるため，温度が変わらない限り一定の値となる。
また、沈殿がある以上、もうこれ以上解けることができない状態であり、溶解平衡の状態の水溶液は、飽和溶液となっている。
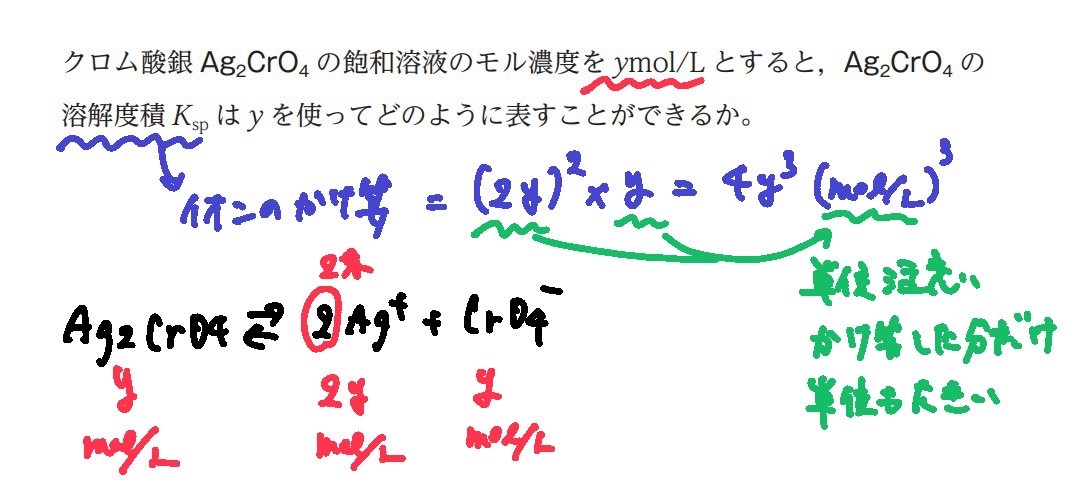
溶解度積を使った計算
Ksp ＝ [Ag+][Cl－] という公式にあてはめていくが、濃度は電離式の係数を使う。
①１つをモル濃度をｘと置く
②電離式から、係数比を求めて、モル比がわかり、もう１つの方もｘで表現できる
③さらに係数比のところが指数乗になる
④それらを掛け算する
⑤単位に注意
【高校化学】溶解度積を使った計算
共通イオン効果とは
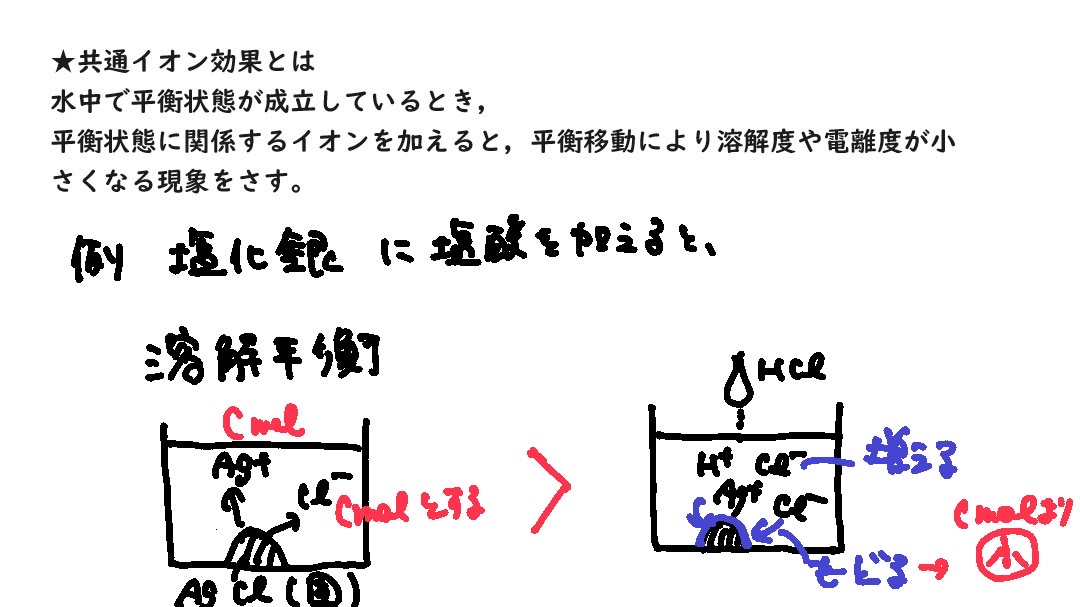
共通イオン効果とは
水中で平衡状態が成立しているとき，平衡状態に関係するイオンを加えると，平衡移動により溶解度や電離度が小さくなる現象。
例 AgCl の溶解平衡状態『AgCl（固） ⇄ Ag+ + Cl－』に、
0.10mol/L の塩酸を加えると、
溶解平衡状態なので、Ag+もCl-も飽和状態で溶けているが、
さらに電離度1の強酸HClを加えると、さらにCl-が解けることになり、
Cl－を減らすために、左向きの反応が進む。
これによって、もともとのAg+とCl-のセット（AgCl）が析出する（もともとのAg+とCl-の濃度が減る。ただしCl-は塩酸の分追加されているが。）という効果
【高校化学】共通イオン効果とは
共通イオン効果（硫化物の沈殿を操作できる）
例 硫化亜鉛 ZnSと、硫化水素H2Sの混合物
Z n S( 固 ) ⇄ Z n 2 + + S 2 − …①
H2S ⇄ 2H+ + S2 − …②
この混合物に、酸性（H+）を追加したり、塩基性（OH-）を追加したり、pH を調整することで，硫化物Z n Sの溶解平衡を操作することができる。
★硫化物Z n Sの沈殿を減らしたい場合
H+を追加《pHを２くらいまでやると、Z n S（固体）がなくなる》
→②の式がH+を減少する方向に反応し、S2-もセットで減少
→S2-を増加させるため、①の式で硫化物Z n S（固体）が電離し溶けていく
★硫化物の沈殿Z n Sを増やしたい場合
OH-を追加
→②の式でH+がOH-とくっついて減少し、H+を増加させるために右反応が進む（S2-が増加）
→S2-を減少させるために、①の式でZ n S（固体）が析出
【高校化学】共通イオン効果（硫化物の沈殿を操作できる）
共通イオン効果（モール法）
★モール法とは
塩化物イオンがどのくらいあるかを定量（測定）する方法
手順
水溶液中にCl- 、指示薬としてクロム酸カリウム K2CrO4 を滴下
水中には、Cl- + CrO4 2- のイオンが存在
ここに銀イオンAg+（硝酸銀水溶液AgNO3）を滴下すると、
銀イオンはCl- か、 CrO4 2- と反応し、それぞれ塩化銀AgCl と クロム酸銀Ag2CrO4（赤褐色の沈殿） のどちらかができる可能性があるが、
溶解度積の値が 『塩化銀AgCl ＜ クロム酸銀Ag2CrO4』なので、
先に飽和を迎えて析出するのが塩化銀AgClとなる。
水中の塩化物イオンがなくなると、クロム酸銀Ag2CrO4が析出すると赤褐色の沈殿が現れるので、そこで銀イオンAg+の滴下を終了する。
クロム酸銀Ag2CrO4が析出し始める＝水溶液中の塩化物イオンがなくなる＝銀イオンAg+の滴下量
あとは、銀イオンAg+の滴下量を調べれば、塩化物イオンがどのくらいあるかを定量（測定）できる。